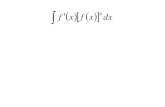The Derivative-Instantaneous rate of change

0( ) ( )

( ) limhdy f a h f a

f adx h

0( ) ( )

( ) limhdy f x h f x

f xdx h

The derivative of a function, f at a specific value of x, say a is a value given by:

The derivative of a function, f as a function of x, is called f (x) and is given by:

0( ) ( )

( ) limhdy f x h f x

f xdx h

2( ) 3 4 7f x x x

2

2 2

( ) 3( ) 4( ) 7

3 6 3 4 4 7

f x h x h x h

x xh h x h

Find the derivative of

2 2 2

0(3 6 3 4 4 7) (3 4 7)

limhx xh h x h x x

h

2

0 06 3 4 (6 3 4)

lim limh hxh h h h x h

h h

0lim 6 3 4 6 4h x h x

( ) 6 4f x x

Related problems 2( ) 3 4 7f x x x

1) Find the slope of f (x) at x = 3, x = -2

3) Find the point on f (x) for which the slope is 2

4) Find the point for which f (x) has a horizontal tangent line

2) Write the equation of the tangent line at x = -2

Solutions 2( ) 3 4 7f x x x

1) Find the slope of f (x) at x = 3, x = -2

2) Write the equation of the tangent line at x = -2

( ) 6 4f x x so

( 2) 6( 2) 4 16f

(3) 6(3) 4 14f

1 1( )y y m x x 2( 2) 3( 2) 4( 2) 7 27f

27 16( 2)y x

27 16( 2)y x 16 5y x

use the point-slope formula

Find the value of y

Solutions 2( ) 3 4 7f x x x

3) Find the point on f (x) for which the slope is 2

4) Find the point for which f (x) has a horizontal tangent line

( ) 6 4f x x 6 4 2

1

x

x

2

3x

2(1) 3(1) 4(1) 7 6f The point is (1, 6)

6 4 0x

22 2 2 17( ) 3( ) 4( ) 73 3 3 3

f The point is (2/3, 17/3)

Figure 2.7: Derivatives at endpoints are one-sided limits.

Derivatives at Endpoints are one-sided limits.

How a derivative can fail to exist

A cornerA vertical tangent

A discontinuity

Which of the three examples are the functionscontinuous?

The graph of a function

The graph of the derivative (slope) of the function

Where f(x) is increasing(slope is positive)

Where f(x) is decreasing(Slope is negative)

Horizontal tangent (slope =0)

3.3 Differentiation formulas

Simple Power rule 1n ndx nx

dx

Sum and difference rule ( ) ( )d d d

u v u vdx dx dx

Constant multiple rule ( )d d

cu c udx dx

Constant ( ) 0d

cdx

Find the derivative function for:2 1

( ) 175 3

xf x

x

2( ) (3 2)f x x

12 21 1

( ) 175 3

f x x x

32

2 1( )

56

f x x

x

2( ) 9 12 4f x x x

( ) 18 12f x x

rewrite

rewrite

321 1 1

( ) 2* ( )( ) 05 3 2

f x x x

Rules for Finding Derivativesu and v are functions of x.

Simple Power rule 1n ndx nx

dx

Sum and difference rule ( ) ( )d d d

u v u vdx dx dx

Constant multiple rule ( )d d

cu c udx dx

Product rule ( ) ( )d d d

uv u v v udx dx dx

Quotient rule2

( ) ( )d d

v u u vd u dx dxdx v v

Differentiate2 1 3(3 2 )(4 5)y x x x

( ) ( )d d d

uv u v v udx dx dx

2 1 3 3 2 1(3 2 ) (4 5) (4 5) (3 2 )dy d d

x x x x x xdx dx dx

2 1 2 3 2(3 2 )(12 ) (4 5)(6 2 )dy

x x x x x xdx

4 4 2

4 2

36 24 24 8 30 10

60 14 10

dyx x x x x x

dxdy

x x xdx

Product rule

Differentiate 2

5 2

1

xy

x

2 2

2 2

( 1) (5 2) (5 2) ( 1)

( 1)

d dx x x xdy dx dx

dx x

2

( ) ( )d d

v u u vd u dx dxdx v v

2

2 2

( 1)(5) (5 2)(2 )

( 1)

dy x x x

dx x

2 2

2 2

(5 5) (10 4 )

( 1)

dy x x x

dx x

2

2 2

5 4 5

( 1)

dy x x

dx x

Quotient rule

Find the derivative function for:2( ) (3 2 )(5 4 )f x x x x

2

5 2( )

1

xf x

x

2 2( ) (3 2 ) (5 4 ) (5 4 ) (3 2 )d d

f x x x x x x xdx dx

2(3 2 )4 (5 4 )(3 4 )x x x x

224 4 15x x

2 2

2 2

( 1) (5 2) (5 2) ( 1)( )

( 1)

d dx x x x

dx dxf xx

2 2 2

2 2 2 2

2

2 2

( 1)5 (5 2)2 (5 5) (10 4 )

( 1) ( 1)

5 4 5

( 1)

x x x x x x

x

x x

xx

Velocity. The particle is moving forward for the first 3 seconds and backwards the next 2 sec, stands still for a second and then moves forward.

forward motion means velocity is positive

backward motion means velocity is negative

If velocity = 0, object is standing still.

The graphs of s and v as functions of time; s is largest when v = ds/dt = 0. The graph of s is not the path of the rock: It is a plot of height versus time. The slope of the plot is the rock’s velocity graphed here as a straight line.

a) How high does the rock go?

b) What is the velocity when the rock is 256 ft. above the ground on the way up? On the way down?c) What is the acceleration of the rock at any time?

d) When does the rock hit the ground? At what velocity?

3.4 applications

A dynamite blast blows a heavy rock straight up with a launch velocity of 160 ft/sec. Its height is given by s = -16t2 +160t.

A dynamite blast blows a heavy rock straight up with a launch velocity of 160 ft/sec. Its height is given by s = -16t2 +160t.

a) How high does the rock go?Maximum height occurs when v =0.

-32t + 160 = 0v = s´= -32t + 160

t = 5 sec.

s = -16t2 +160t

At t = 5, s = -16(5)2 +160(5) = 400 feet.

A dynamite blast blows a heavy rock straight up with a launch velocity of 160 ft/sec. Its height is given by s = -16t2 +160t.

b) What is the velocity when the rock is 256 ft. above the ground on the way up? On the way down?

v =-32t + 160at t = 2v=-32(2)+160 = 96 ft/sec.at t = 8v=-32(8)+160 = -96 ft/sec

-16t2 +160t = 256-16t2 +160t –256=0-16(t2 - 10t + 16)=0-16(t – 2) (t- 8) = 0t = 2 or t = 8

Find the times

Substitute the timesinto the velocityfunction

Set position = 256

A dynamite blast blows a heavy rock straight up with a launch velocity of 160 ft/sec. Its height is given by s = -16t2 +160t.

c) What is the acceleration of the rock at any time?

d) When does the rock hit the ground? At what velocity?

s = -16t2 +160t

v = s´= -32t + 160

a = v´ = s´´= -32ft/sec2

s = -16t2 +160t = 0t = 0 and t = 10

v =-32t + 160v = -32(10)+ 160 = -160 ft/sec.

Set position = 0

3.5 Derivatives of trig functions-formulas needed

sin(x+h) = sin x*cos h+cos x*sin h

0

sinhlim 1h h

cos(x+h) = cos x*cos h- sin x*sin h

0

cos 1lim 0h

h

h

Derivative of y = sin x0

( ) ( )( ) limh

dy f x h f xf x

dx h

0sin( ) sin( )

( ) limhx h x

f xh

0sin( )cos( ) cos( )sin( ) sin( )

limhx h x h x

h

0sin( )cos( ) sin( ) cos( )sin( )

limhx h x x h

h

0sin( )(cos( ) 1) cos( )sin( )

limhx h x h

h h

0sin( )(cos( ) 1) cos( )sin( )

limhx h x h

h h

0 +cos(x)*1 = cos (x)

3.5 Derivatives of Trigonometric Functions

sin cosd

x xdx

cos sind

x xdx

2tan secd

x xdx

2cot cscd

x xdx

sec sec tand

x x xdx

csc csc cotd

x x xdx

Figure 25: The curve y´ = –sin x as the graph of the slopes of the tangents to the curve y = cos x.

Slope of y = cos x

Find the derivatives21

( ) 5sin sec tan 7 32

f x x x x x x

21( ) 5cos sec tan sec tan (1) 14

2f x x x x x x x x

1 sin( )

cos

xf x

x x

2

( cos ) (1 sin ) (1 sin ) ( cos )( )

( cos )

d dx x x x x x

dx dxf xx x

2

( cos )(cos ) (1 sin )(1 sin )( )

( cos )

x x x x xf x

x x

2 2 2 2

2 2

( cos cos ) (1 sin ) cos cos 1 sin( )

( cos ) ( cos )

x x x x x x x xf x

x x x x

2

cos( )

( cos )

x xf x

x x