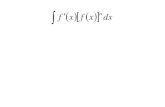3.2 Derivative as a Function

AP Calculus

Derivative at a Point x = a

Derivative f’ (a) for specific values of a

Derivative as a Function

Function f’ (x)

Domain and Differentiability

Domain of f’ (x) is all values of x in domain of

f (x) for which the limit exists. F’ (x) is differentiable on (a, b) if f

‘(x) exists for all x in (a, b). If f’ (x) exists for all x, then f (x) is

differentiable.

Example 1

Prove that f (x) = x3 – 12x is differentiable. Compute f ‘(x) and write the equation of the tangent line at x = -3.

Solution

F ‘(x) = 3x2 – 12 Equation of tangent line at x = -3

y = 15x + 54

Example 2

Calculate the derivative of y = x-2. Find the domain of y and y’

Example 2

Solution: y’ = -2x-3

Domain of y: {x| x ≠ 0} Domain of y’ : {x| x ≠ 0} The function is differentiable.

Leibniz Notation

Another notation for writing the derivative:

Read “dy dx” For the last example y = x-2, the

solution could have been written this way:

Theorem 1: Power Rule

For all exponents n,

Power Rule Examples

Example 3

Calculate the derivative of the function below

Example 3

Solution:

Theorem 2

Assume that f and g are differentiable functions.

Sum Rule: the function f + g is differentiable (f + g)’ = f’ + g’

Constant Multiple Rule: For any constant c, cf is differentiable and

(cf)’ = cf’

Example 4

Find the points on the graph of f(t) = t3 – 12t + 4 where the tangent line(s) is horizontal.

Example 4

Solution:

Graphical Insight

How is the graph of f(x) = x3 – 12x related to the graph of f’(x) = 3x2 – 12 ?

f(x) = x3 – 12 x

f’(x) = 3x2 - 12

Increasing on (-∞, -2)

Graph of f’(x) positive on (-∞, -2)

Zeros at -2, 2

Decreasing on (-2, 2)

f’(x) is negative on (-2,2)

Increasing on (2, ∞)

f’(x) is positive on (2, ∞)

What happens to f(x) at x = -2 and x = 2??

Theorem 3

Differentiability Implies Continuity If f is differentiable at x = c, then f is

continuous at x = c.

Example 5

Show that f(x) = |x| is continuous but not differentiable at x = 0.

Example 5 - Solution

The function is continuous at x = 0 because

Example 5 - Solution

The one-sided limits are not equal:

The function is not differentiable at x = 0

Graphical Insight

Local Linearity f(x) = x3 – 12x

Graphical Insight

g(x) = |x|

Example 6

Show that f(x) = x 1/3 is not differentiable at x = 0.

Example 6 - Solution

f’(0) =

The limit at x = 0 is infinite

The slope of the tangent line is infinite – vertical tangent line