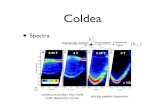
Real Spin in Pseudospin Quasiparticles of Bilayer Quantum Hall systems
Sponsors - usherbrooke.ca · 2. The standard approaches : - Quasiparticles, Fermi surface, Fermi...
Transcript of Sponsors - usherbrooke.ca · 2. The standard approaches : - Quasiparticles, Fermi surface, Fermi...
-
1
Electronic correlations
André-Marie Tremblay
Sponsors:
CENTRE DE RECHERCHE SUR LES PROPRIÉTÉS ÉLECTRONIQUES
DE MATÉRIAUX AVANCÉS
-
Steve Allen (PhD)
Bumsoo Kyung (postdoc)
Yury Vilk (now at Chicago)
Acknowledgements:
Samuel Moukouri (postdoc)
François Lemay (PhD)
David Poulin
Hugo Touchette
Liang Chen (now at U. Ottawa)
-
4
1. Motivation
H = kinetic + Coulomb
- Many new ideas and concepts needed for progress(Born-Oppenheimer, H-F, Bands...)
- Successfull program - Semiconductors, metals- Magnets
- Is there anything left to do?- Unexplained materials: High Tc, Organics...- Strong correlations:
strong interactions, low dimension
Theory of solids
-
5
Outline 1. Motivation
2. The standard approaches : - Quasiparticles, Fermi surface, Fermi liquid- Fermi liquids and phase transitions- Heisenberg and related
3. Experimental evidence for failure :- d=1 spin-charge separation- d=2 disappearing act of Fermi surface
4. Theoretical reasons for failure :- Effects of strong coupling - Effects of low d in weak to intermediate coupling
-
6
5. The Hubbard model
6. A non-perturbative approach (U > 0 and U < 0 )- Proof that it works- How it works
7. Results:- Mechanism for pseudogap- Spectral weight rearrangement
8. Conclusion.
-
7
2. The standard approaches :
A. Quasiparticles, Fermi surface and Fermi liquids- LDA (Nobel prize 1998)
L.F. Mattheiss, Phys. Rev. Lett. 58, 1028 (1987).
La2CuO4
-
8
2. The standard approaches :
- Matrix elements of H in LDA basis- In practice, from general considerations:
- Short range- Single Slater determinant not eigenstate
- Phase space + Pauli restricts possible scatterings:- Quasiparticles m*, effective fields,
- «See» the quasiparticles with ARPES: ePhoton
= E + ω + µµµµ - W k2m
2
k
ph
-
9
R. Claessen, R.O.Anderson, J.W. Allen,C.G. Olson, C.Janowitz, W.P. Ellis,S. Harm, M. Kalning,R. Manzke,and M. Skibowski,Phys. Rev. Lett. 69,808 (1992).
-
10
T. Valla, A. V. Fedorov, P. D. Johnson, and S. L. HulbertP.R.L. 83, 2085 (1999).
-
11
2. The standard approaches :
B. Thermodynamics and phase transitions
- Thermodynamics of Fermi liquids -particle-hole excitations
- Phase transitionsχ ∼ N(0) / ( 1 + Foa)
- Superconducting transition
C. Heisenberg model and related models
- Band for s-p- Localized (often) for d-f
Only spin degrees of freedomUse symmetry to write H
-
123. Experimental evidence for failure : - d=1 spin-charge separation
C. Bourbonnaiset al.(cond-mat/9903101).
-
13
3. Experimental evidence for failure :
- d=2 partial vanishing act of the Fermi surface.
D.S. Marshall, D.S. Dessau, A.G.Loeser, C.-H. Park,A.Y. Matsuura, J.N. Eckstein, I.Bozovic, P. Fournier,A. Kapitulnik, W.E. Spicer, andZ.X. Shen, Phys. Rev.Lett. 76, 4841 (1996).
-
14
Optimally doped BISCCONormal Superconductor
A. V. Fedorov, T. Valla, P. D. Johnson et al. P.R.L. 82, 2179 (1999)
-
15
d = 2, Mermin-Wagner
(rµ)2! q2µqµ¡q
Dµ2E/Zd2q
kT
q2!1
4. Theoretical reasons for failure :
A. Strong interactions (localized states)
B. Thermal and quantum fluctuations in d = 2
d = 1 : R.G., Bosonization, Conformal Field Theory...d = 2 : Slave bosons, R.G., strong coupling p.t., TPSC
-
16
H = ¡ X¾
ti;j³cyi¾cj¾ + c
yj¾ci¾
´+ U
Xi
ni"ni#
5. Hubbard model (Kanamori, Gutzwiller, 1963) :
tU
- Screened interaction U- U, T, n- a = 1, t = 1, h = 1
- 2001 vs 1963: Numerical solutions to check analytical approaches
t
t
-
17
A(k,ω)
ω- U/2 U/2
ω
k
π/a−π/a
ω
k
π/a−π/a
ω
A(k,ω)
- 4 t
ω
A(k,ω)
+ 4 t
U = 0 t = 0
U
-U/2
+U/2
0
-
18
-
19http://www.physique.usherb.ca/~tremblay/articles/PiC.pdfFor first part of this talk :
S. Lefebvre, P. Wzietek, S. Brown, C. Bourbonnais, D. Jérome, C. Mézière, M. Fourmigué, and P. Batail
-
20
6. A non-perturbative approach for both U > 0 and U < 0
q0.0
0.4
(0,0) (π,π)(π,0) (0,0) q0
20.0
0.4
0
2
n S c
h(q)
n S s
p(q)
U = 8
U = 8
U = 4
U = 4n = 0.26
n = 0.94n = 0.60
n = 0.45n = 0.20
n = 0.80n = 0.33n = 0.19
n = 1.0n = 0.45n = 0.20
(a)
(b) (c)
(d)
U > 0
QMC + cal.: Vilk et al. P.R. B 49, 13267 (1994)
Notes: -F.L. parameters-Self also Fermi-liquid
- Proofs that it works
-
21
0.50 0.75 1.00T
0.0
0.5
1.0
1.5
2.0U=4.0n=0.87
Monte Carlo
8x8 (BWS)
8*8 (BW)
This work
FLEX no AL
FLEX
π,π
χ(
,0)
sp
U = + 4
QMC: Bulut, Scalapino, White, P.R. B 50, 9623 (1994).Calc.: Vilk, et al. J. Phys. I France, 7, 1309 (1997).
Proofs...
-
22
-5.00 0.00 5.00 -5.00 0.00 5.00ω/t
(0,0)
(0, )π
( , )π2π2
( , )π π4 4( , )π π4 2
(0,0) (0, )π
( ,0)π
Monte Carlo Many-Body
-5.00 0.00 5.00
Flex
U = + 4
Calc. + QMC: Moukouri et al. P.R. B 61, 7887 (2000).
Proofs...
-
23
-1 0 10.0
0.5
1.0
A(ω
)
-1 0 1 -1 0 1
Monte Carlo Many-Body Σ(s) FLEX
-0.5
0.0
G(τ
)
0 β
a) b) c)L=4
L=6
L=8
L=10
β/2
U = + 4
Calc. + QMC: Moukouri et al. P.R. B 61, 7887 (2000).
Proofs...
-
24
I
II ωωωω
kF
A(ωωωω)
E
k
A(ωωωω)
ωωωω
kF
III
99-aps/Explication...
E
k
A(ωωωω)
ωωωω
kF
TX
T = 0nc
T
kF
kF
2∆2∆
-
25
U = - 4
Calc. : Kyung et al. cond-mat/0010001QMC : Moreo, Scalapino, White, P.R. B. 45, 7544 (1992)
Moving to the attractive case....
Proofs...
-
26
U = - 4
Calc. : Kyung et al. cond-mat/0010001QMC : Trivedi and Randeria, P.R. L. 75, 312 (1995)
2nd order perturbation theory
S.C. T-matrix
Proofs...
-
27
-4.0 0.0 4.0ω
0.0
0.2
0.4T = 0.25, n = 0.8, U = -4
QMCMany-Body
-4.0 0.0 4.0ω
0.0
0.4
0.8
1.2N( )ω A(k, )ω
(a) (b)
(c) (d)
-4.0 0.0 4.00.0
0.1
0.2
0.3T = 0.2, n=0.8, U = -4
Many-BodyQMC
-4.0 0.0 4.00.0
0.2
0.4
0.6
τ-0.6
-0.4
-0.2
0.0
T = 0.25, n = 0.8, U = -4QMC
Many Body
τ-0.6
-0.4
-0.2
0.0G(k, )τ G(k, )τ
(a) (b)
(c) (d)
-0.6
-0.4
-0.2
0.0
T = 0.2, n=0.8, U = -4
Many-Body
QMC
-0.6
-0.4
-0.2
0.0
Σk
U = - 4
Kyung et al. cond-mat/0010001
Proofs...
-
28
§(1)¾
³1; 1
´G(1)¾
³1; 2
´= AG
(1)¡¾
³1; 1+
´G(1)¾ (1; 2)
where A depends on external ¯eld and is chosen such that the exact result
§¾³1; 1
´G¾
³1; 1+
´= U
Dn"n#
Eis satis¯ed. One ¯nds
A = U
Dn"n#
EDn"E Dn#E
Functional derivative ofDn"n#
E=³Dn"E Dn#E´drops out of spin vertex
Usp = A = U
Dn"n#
EDn"E Dn#E
First step: Two-Particle Self-ConsistentHow it works...
-
29
To close the system of equations, while satisfying conservation laws and
the Pauli principle¿³n" ¡ n#
´2À=
Dn"E+Dn#E¡ 2
Dn"n#
ET
N
Xeq
Â0(q)
1¡ 12UspÂ0(q)= n¡ 2hn"n#i (1)
Recall
Usp = U
Dn"n#
EDn"E Dn#E (2)
To have charge °uctuations that satisfy Pauli principle as well,
T
N
Xq
Â0(q)
1 + 12UchÂ0(q)= n+ 2hn"n#i ¡ n2 (3)
(Bonus: Mermin-Wagner theorem)
How it works...
-
30
§¾³1; 1
´G¾
³1; 2
´= ¡U
DÃy¡¾
³1+´Ã¡¾ (1)þ (1)Ãy¾ (2)
EÁ
§¾³1; 1
´G¾
³1; 2
´= ¡U
"±G¾ (1; 2)
±Á¡¾ (1+; 1)¡G¡¾
³1; 1+
´G¾ (1; 2)
#
Last term is Hartree Fock (lim! ! 1). Multiply by G¡1, replace lowerenergy part results of TPSC
§(2)¾ (1; 2) = UG
(1)¡¾
³1; 1+
´± (1¡ 2)¡ UG(1)
"±§(1)
±G(1)±G(1)
±Á
#Transverse+longitudinal for crossing-symmetry
§(2)¾ (k) = Un¡¾ +
U
8
T
N
Xq
h3UspÂ
(1)(q) + UchÂ(1)(q)
iG(1)¾ (k+ q): (4)
Second step: improved self-energyHow it works...
-
31
= +
1
32 2
1
33
12
2
3
4
5
=Σ1 2 +
-
2
45
2
1
1
21
-
32
Results of the analogous procedure for U < 0
Upp = Uh(1¡ n")n#ih1¡ n"ihn#i
: (5)
Â(1)p (q) =
Â(1)0 (q)
1 + UppÂ(1)0 (q)
(6)
T
N
XqÂ(1)p (q) exp(¡iqn0¡) = h¢y¢i = hn"n#i : (7)
§(1) ' U2¡ Upp (1¡ n)
2(8)
§(2)¾ (k) = Un¡¾ ¡ U T
N
XqUppÂ
(1)p (q)G
(1)¡¾(q ¡ k) (9)
-
33
Satis¯es Pauli principle and generalization of f¡sum ruleZd!
¼ImÂ(1) (q; !) =
Dh¢q (0) ;¢
yq (0)
iE= 1¡ n ; 8q (10)
Zd!
¼! ImÂ(1) (q; !) =
24 1N
Xk
³"k + "¡k+q
´ ³1¡ 2
Dnk"
E´35 (11)¡2
µ¹(1) ¡ U
2
¶(1¡ n) ; 8q (12)
Internal accuracy check (For both U > 0 and U < 0).
1
2Trh§(2)G(1)
i= lim
¿!0¡T
N
Xk
§(2)¾ (k)G
(1)¾ (k) e
¡ikn¿ = UDn"n#
ECheck : Tr
h§(2)G(1)
i~ Tr
h§(2)G(2)
i
-
34
U = - 47. Results:
- Mechanism for pseudogap
- Enter the renormalized-classical regime. N.B. d = 2
- (analogous to U > 0 ) : Vilk et al. Europhys. Lett. 33, 159 (1996) Pines, Schmalian (98)
32
-
35
U = - 47. Results:
- Mechanism for pseudogap
- Pairing correlation length larger than single-particle thermal de Broglie wavelength (vF / T)
ξ ∼ 1.3 ξth
-
36
0.00 0.50 1.00 1.50 2.00ω
T=1/3
T=1/4
T=1/5
Even part of the pair susceptibility at q = 0, for different temperatures
U = - 4
Allen, et al. P.R. L 83, 4128 (1999)
Mechanism for pseudogap formation in the attractive model:
d = 2 is crucial
-
37
U = - 47. Results:
- Spectral weight rearrangement
- Pseudogap appears first in total density of states- Fills in instead of opening up- Rearrangement over huge frequency scale compared with either T or ∆ T. (∆ T ~ 0.03, T ~ 0.2, ∆ω ∼ 1 )
-
38
U = - 47. Results:
- Crossover diagram
-
39
8. Conclusion :
U > 0
- Evidence against renormalized classical regime for spin fluctuations in pseudogap regime.
Philippe Bourges cond-mat/0009373
T
δ
pseudogap
AF
SC QCP ?
-
40
- Quantum critical point, d = 2: - Instability at incommensurate q- Largest doping : 0.315
Freericks, Jarrell cond-mat/9405025
d = infinity
U < W
U > W
U > 0 Tδ
U SDW?
0.3
U
U
Vilk et al. P.R. B 49, 13267 (1994)
- Decreases with increasing U
-
41
- Slightly Overdoped High-Tc Superconductor TlSr2CaCu2O6.8Guo-qing Zheng et al., P. R. L. 85, 405 (2000) - Pseudogap in Knight shift and NMR relaxation strongly H dependent, contrary to underdoped (up to 23 T).
- Underdoped in a range ∆Τ ∼ 15 Κ near Tc see evidence for renormalized classical regime (KT behavior).
Corson et al.Nature, 398, 221 (1999).
- Higher symmetry group creates large range of T where there is a pseudogap.
n = 1 n = 0
SO(2)
KT
Pseudogap
T
SO(3)Allen et al. P.R.L. 83, 4128 (1999)
U < 0 Pairing-fluctuation induced pseudogap
-
42
- How can we understand electronic systems that show both localized and extended character?- Why do both organic and high-temperature superconductors show broken-symmetry states where mean-field-like quasipar- ticles seem to reappear? - Why is the condensate fraction in this case smaller than what would be expected from the shape of the would-be Fermi surface in the normal state? - Are there new elementary excitations that could summarize and explain in a simple way the anomalous properties of these systems? - Do quantum critical points play an important role in the Physics of these systems?- Are there new types of broken symmetries? - How do we build a theoretical approach that can include both strong-coupling and d = 2 fluctuation effects? - What is the origin of d-wave superconductivity in the high- temperature superconductors?