http://www.teacherspayteachers.com/Store/Teachmehowtoalge

http://www.facebook.com/teachmehowtoALGE

So what is a system and why is it messing with our l inear equations?

Systems of Linear EquationsOb

jecti

ves: After this lesson I will be able to solve a system of equation by graphing.

After this lesson I will be able to identify the number of solutions a system of equation has, by graphing.

1

2

SOLVE SYSTEMS BY GRAPHING

A system of linear equations is when two lines “work together” or touch when graphed on the same coordinate plane.

A system is when many things work together. We see examples of systems ALL THE TIME in science class! The WATER CYCLE is a system because everything has to work together!

+ =

If they do “touch”, the point(s) at which they touch are the solution(s) :

( x , y )

teachmehowtoALGE

EXPLORE: How many ways can straight lines cross? TRy using your arms:

Your left arm as one LINEAR EQUATION,and the right arm as the other LINEAR EQUATION.

How many ways can you get them to cross?

Well, we know we can DEFINITELY have our arms NEVER touching! If we graph two lines on the same coordinate plane and they do not cross, we say the system consists of two parallel lines and has NO solutions.

SCENARIO 1 :

We also OBVIOUSLY know that we can have our arms cross only at one point! If we graph two lines on the same coordinate plane and they cross at one points, we say that point (x,y) is the solution to the system of linear equations.

SCENARIO 2:

But did you think of the scenario where your arms would be lying on top of one another?This is when a system has an infinite amount of solutions. HINT - it means the lines are the same.

SCENARIO 3:

No Solutions

One Solution

Infinite Solutions

teachmehowtoALGE

Systems of Linear Equationsg r a p h i n g

Keep in mind, SYSTEMS OF LINEAR EQUATIONS allow for us to evaluate two linear equations at the same time!!!

Remember how we found out how many solutions a system had by using our arms?

NONE ONE INFINITEUse the graph to the right to determine whether the system of linear equations has NONE, ONE, or INFINITE solutions.PRACTICE:

y = -x - 3y = x - 1

2x + 2y = -6y = -x - 3

y = -x - 32x + 2y = 4

2x + 2y = -63x + y = 3

1 2

3 4 y = x - 1

2x + 2y = -6

y = -x - 3

3x + y = 32x + 2y = 4

ANSWER: ANSWER:

ANSWER: ANSWER:

teachmehowtoALGE

Sometimes they will make us graph our own linear equations to discover how many solutions the system has.

y = -2x + 1y = 3x - 1

y = -2x - 1y = -2x + 2

Exercises

Example

Less

on

5-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

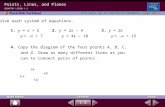
Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

y = 1/2x + 0y = -2/3x - 1

y = -2x + 6y = 2x + 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

y = 2/3x + 3y = 2/3x - 2

y = -2x + 2y = -2x + 2

Exercises

Example

Less

on

5-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

PR

AC

TI

CE 5 6

ANSWER: ANSWER:

7 8

ANSWER: ANSWER:

9

ANSWER:

10

ANSWER:

teachmehowtoALGE

4 y = 3x - 4 y = -3x + 2

5 y = 1/3x + 3 y = -2/3x - 3

6 y = 5/4x - 2 y = 5/4x - 1

Practice on your own:Graphing Systems of Linear Equations

ANSWER:

Use the graph below to determine whether the system of linear equations has NONE, ONE, or INFINITE solutions.

y = -x + 2y = x + 1

y = -x + 23x + 3y = -3

3x + 3y = -3y = -x - 1

1 2

3

y = -x - 1

3x + 3y = -3

y = x + 1y = -x + 2

ANSWER: ANSWER:

ANSWER:

Graph the systems below, stating how many solutions the system has:

ANSWER: ANSWER:

teachmehowtoALGE

So what is a system and why is it messing with our l inear equations?

Systems of Linear EquationsOb

jecti

ves: After this lesson I will be able to solve a system of equation by graphing.

After this lesson I will be able to identify the number of solutions a system of equation has, by graphing.

1

2

SOLVE SYSTEMS BY GRAPHING

A system of linear equations is when two lines “work together” or touch when graphed on the same coordinate plane.

A system is when many things work together. We see examples of systems ALL THE TIME in science class! The WATER CYCLE is a system because everything has to work together!

+ =

If they do “touch”, the point(s) at which they touch are the solution(s) :

( x , y )

teachmehowtoALGE

CONDENSATION

PERCIPITATION

PERCIPITATION

COLLECTION

EVAPORATION

EVAPORATION

Systems of Linear Equationsg r a p h i n g

Keep in mind, SYSTEMS OF LINEAR EQUATIONS allow for us to evaluate two linear equations at the same time!!!

Remember how we found out how many solutions a system had by using our arms?

NONE ONE INFINITEUse the graph to the right to determine whether the system of linear equations has NONE, ONE, or INFINITE solutions.PRACTICE:

y = -x - 3y = x - 1

2x + 2y = -6y = -x - 3

y = -x - 32x + 2y = 4

2x + 2y = -63x + y = 3

1 2

3 4 y = x - 1

2x + 2y = -6

y = -x - 3

3x + y = 32x + 2y = 4

ANSWER: ANSWER:

ANSWER: ANSWER:

ONE INFINITE

NONE ONE

teachmehowtoALGE

Sometimes they will make us graph our own linear equations to discover how many solutions the system has.

y = -2x + 1y = 3x - 1

y = -2x - 1y = -2x + 2

Exercises

Example

Less

on

5-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

y = 1/2x + 0y = -2/3x - 1

y = -2x + 6y = 2x + 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

y = 2/3x + 3y = 2/3x - 2

y = -2x + 2y = -2x + 2

Exercises

Example

Less

on

5-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

Exercises

Example

Less

on 5

-1

Study Guide and Intervention (continued)

Graphing Systems of Equations

NAME ______________________________________________ DATE______________ PERIOD _____

Chapter 5 7 Glencoe Algebra 1

5-1

Copy

right

©G

lenc

oe/M

cGra

w-Hi

ll, a

divis

ion

of T

he M

cGra

w-Hi

ll Com

pani

es, I

nc.

Solve by Graphing One method of solving a system of equations is to graph theequations on the same coordinate plane.

Graph each system of equations. Then determine whether thesystem has no solution, one solution, or infinitely many solutions. If the system hasone solution, name it.

a. x ! y " 2x # y " 4The graphs intersect. Therefore, there is one solution. The point (3, !1) seems to lie on both lines. Check this estimate by replacing x with 3 and y with !1 in each equation.

x " y # 23 " (!1) # 2

x ! y # 43 ! (!1) # 3 " 1 or 4 The solution is (3, !1).

b. y " 2x ! 12y " 4x ! 2The graphs coincide. Therefore there are infinitely many solutions.

Graph each system of equations. Then determine whether the system has nosolution, one solution, or infinitely many solutions. If the system has one solution,name it.

1. y # !2 2. x # 2 3. y # x3x ! y # !1 2x " y # 1 x " y # 3

4. 2x " y # 6 5. 3x " 2y # 6 6. 2y # !4x " 42x ! y # !2 3x " 2y # !4 y # !2x " 2

x

y

Ox

y

O

x

y

O

x

y

O

x

y

Ox

y

O

1$2

x

y

O

y " 2x ! 1 2y " 4x ! 2

x

y

O (3, –1)

x # y " 4

x ! y " 2

PR

AC

TI

CE 5 6

ANSWER: ANSWER:

7 8

ANSWER: ANSWER:

9

ANSWER:

10

ANSWER:

NONE

NONE

ONE

ONE ONE

INFINITE

teachmehowtoALGE

4 y = 3x - 4 y = -3x + 2

5 y = 1/3x + 3 y = -2/3x - 3

6 y = 5/4x - 2 y = 5/4x - 1

Practice on your own:Graphing Systems of Linear Equations

ANSWER:

Use the graph below to determine whether the system of linear equations has NONE, ONE, or INFINITE solutions.

y = -x + 2y = x + 1

y = -x + 23x + 3y = -3

3x + 3y = -3y = -x - 1

1 2

3

y = -x - 1

3x + 3y = -3

y = x + 1y = -x + 2

ANSWER: ANSWER:

ANSWER:

Graph the systems below, stating how many solutions the system has:

ANSWER: ANSWER:

ONE NONE

INFINITE

ONE ONE NONE

NAME:

teachmehowtoALGE