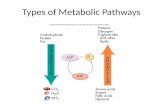
Typical network of metabolic pathways
description
Transcript of Typical network of metabolic pathways

LECTURE 6Topic 1: Metabolic network and stoichiometric matrixTopic 2: Centrality measures of nodes

Typical network of metabolic pathways
Reactions are catalyzed by enzymes. One enzyme molecule usually catalyzes thousands reactions per second (~102-107)
The pathway map may be considered as a static model of metabolism

For a metabolic network consisting of m substances and r reactions the system dynamics is described by systems equations.
The stoichiometric coefficients nij assigned to the substance Si and the reaction vj can be combined into the so called stoichiometric matrix.
What is a stoichiometric matrix?

Example reaction system and corresponding stoichiometric matrix
There are 6 metabolites and 8 reactions in this example system
stoichiometric matrix

Binary form of N
To determine the elementary topological properties, Stiochiometric matrix is also represented as a binary form using the following transformation
nij’=0 if nij =0nij’=1 if nij ≠0

Stiochiometric matrix is a sparse matrix
Source: Systems biology by Bernhard O. Palsson

Information contained in the stiochiometric matrix
Stiochiometric matrix contains many information e.g. about the structure of metabolic network , possible set of steady state fluxes, unbranched reaction pathways etc. 2 simple information:•The number of non-zero entries in column i gives the number of compounds that participate in reaction i.
•The number of non-zero entries in row j gives the number of reactions in which metabolite j participates.
So from the stoicheometric matrix, connectivities of all the metabolites can be computed

Information contained in the stiochiometric matrix
There are relatively few metabolites (24 or so) that are highly connected while most of the metabolites participates in only a few reactions
Source: Systems biology by Bernhard O. Palsson

Information contained in the stiochiometric matrix
In steady state we know that
The right equality sign denotes a linear equation system for determining the rates v
This equation has non trivial solution only for Rank N < r(the number of reactions)
K is called kernel matrix if it satisfies NK=0
The kernel matrix K is not unique

The kernel matrix K of the stoichiometric matrix N that satisfies NK=0, contains (r- Rank N) basis vectors as columns
Every possible set of steady state fluxes can be expressed as a linear combination of the columns of K
Information contained in the stiochiometric matrix

-
With α1= 1 and α2 = 1, , i.e. at steady state v1 =2, v2 =-1 and v3 =-1
Information contained in the stiochiometric matrix
And for steady state flux it holds that J = α1 .k1 + α2.k2
That is v2 and v3 must be in opposite direction of v1 for the steady state corresponding to this kernel matrix which can be easily realized.

Information contained in the stiochiometric matrix
Reaction SystemStoicheometric Matrix
The stoicheomatric matrix comprises r=8 reactions and Rank =5 and thus the kernel matrix has 3 linearly independent columns. A possible solution is as follows:

Information contained in the stiochiometric matrix
Reaction System
The entries in the last row of the kernel matrix is always zero. Hence in steady state the rate of reaction v8 must vanish.

Reaction System
The entries for v3 , v4 and v5 are equal for each column of the kernel matrix, therefore reaction v3 , v4 and v5 constitute an unbranched pathway . In steady state they must have equal rates
Information contained in the stiochiometric matrix
If all basis vectors contain the same entries for a set of rows, this indicate an unbranched reaction path

Elementary flux modes and extreme pathwaysThe definition of the term pathway in a metabolic network is not straightforward.
A descriptive definition of a pathway is a set of subsequent reactions that are in each case linked by common metabolites
Fluxmodes are possible direct routes from one external metabolite to another external metabolite.
A flux mode is an elementary flux mode if it uses a minimal set of reactions and cannot be further decomposed.

Elementary flux modes and extreme pathways

Elementary flux modes and extreme pathways
Extreme pathway is a concept similar to elementary flux modeThe extreme pathways are a subset of elementary flux modes
The difference between the two definitions is the representation of exchange fluxes. If the exchange fluxes are all irreversible the extreme pathways and elementary modes are equivalent
If the exchange fluxes are all reversible there are more elementary flux modes than extreme pathways
One study reported that in human blood cell there are 55 extreme pathways but 6180 elementary flux modes

Elementary flux modes and extreme pathways
Source: Systems biology by Bernhard O Palsson

Elementary flux modes and extreme pathways
Elementary flux modes and extreme pathways can be used to understand the range of metabolic pathways in a network, to test a set of enzymes for production of a desired product and to detect non redundant pathways, to reconstruct metabolism from annotated genome sequences and analyze the effect of enzyme deficiency, to reduce drug effects and to identify drug targets etc.

Centrality measures of nodes

Centrality measuresWithin graph theory and network analysis, there are various measures of the centrality of a vertex within a graph that determine the relative importance of a vertex within the graph.
•Degree centrality•Betweenness centrality•Closeness centrality•Eigenvector centrality•Subgraph centrality
We will discuss on the following centrality measures:

Degree centrality
Degree centrality is defined as the number of links incident upon a node i.e. the number of degree of the node
Degree centrality is often interpreted in terms of the immediate risk of the node for catching whatever is flowing through the network (such as a virus, or some information).
Degree centrality of the blue nodes are higher

Betweenness centrality
The vertex betweenness centrality BC(v) of a vertex v is defined as follows:
Here σuw is the total number of shortest paths between node u and w and σuw(v) is number of shortest paths between node u and w that pass node v
Vertices that occur on many shortest paths between other vertices have higher betweenness than those that do not.

a
db f
e
c
Betweenness centrality σuw σuw(v) σuw/σuw(v)
(a,b) 1 0 0
(a,d) 1 1 1
(a,e) 1 1 1
(a,f) 1 1 1
(b,d) 1 1 1
(b,e) 1 1 1
(b,f) 1 1 1
(d,e) 1 0 0
(d,f) 1 0 0
(e,f) 1 0 0
Betweenness centrality of node c=6
Betweenness centrality of node a=0 Calculation for node c

Hue (from red=0 to blue=max) shows the node betweenness.
Betweenness centrality•Nodes of high betweenness centrality are important for transport. •If they are blocked, transport becomes less efficient and on the other hand if their capacity is improved transport becomes more efficient.•Using a similar concept edge betweenness is calculated.
http://en.wikipedia.org/wiki/Betweenness_centrality#betweenness

Closeness centrality
The farness of a vortex is the sum of the shortest-path distance from the vertex to any other vertex in the graph.The reciprocal of farness is the closeness centrality (CC).
Here, d(v,t) is the shortest distance between vertex v and vertex t
Closeness centrality can be viewed as the efficiency of a vertex in spreading information to all other vertices
vVt
tvdvCC
\
),(1)(

Eigenvector centralityLet A is the adjacency matrix of a graph and λ is the largest eigenvalue of A and x is the corresponding eigenvector then
The ith component of the eigenvector x then gives the eigenvector centrality score of the ith node in the network.
From (1)
N
jjjii xAx
1,
1
•Therefore, for any node, the eigenvector centrality score be proportional to the sum of the scores of all nodes which are connected to it. •Consequently, a node has high value of EC either if it is connected to many other nodes or if it is connected to others that themselves have high EC
-----(1)N×N N×1 N×1
|A-λI|=0, where I is an identity matrix

Subgraph centrality
the number of closed walks of length k starting and ending on vertex i in the network is given by the local spectral moments μ k (i), which are simply defined as the ith diagonal entry of the kth power of the adjacency matrix, A:
Closed walks can be trivial or nontrivial and are directly related to the subgraphs of the network.
Subgraph Centrality in Complex Networks, Physical Review E 71, 056103(2005)

0 1 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 1 0 1 0 0 0 0 0 0 0 0
0 1 0 1 1 1 0 0 0 0 0 0 0 0
0 1 1 0 1 1 0 1 0 0 0 0 0 0
0 0 1 1 0 1 0 0 0 0 0 0 0 0
0 1 1 1 1 0 1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 1 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 1 0 1 0 0 1 1
0 0 0 0 0 0 0 0 1 0 1 0 1 1
0 0 0 0 0 0 1 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1 1 0 1 0 1
0 0 0 0 0 0 0 0 1 1 0 0 1 0
M =
Muv = 1 if there is an edge between nodes u and v and 0 otherwise.
Subgraph centrality
Adjacency matrix

1 0 1 1 0 1 0 0 0 0 0 0 0 0
0 4 2 2 3 2 1 1 0 0 0 0 0 0
1 2 4 3 2 3 1 1 0 0 0 0 0 0
1 2 3 5 2 3 1 0 1 0 0 0 0 0
0 3 2 2 3 2 1 1 0 0 0 0 0 0
1 2 3 3 2 5 0 1 0 0 1 0 0 0
0 1 1 1 1 0 2 0 0 1 0 0 0 0
0 1 1 0 1 1 0 2 0 1 0 0 1 1
0 0 0 1 0 0 0 0 4 2 1 1 2 2
0 0 0 0 0 0 1 1 2 4 0 1 2 2
0 0 0 0 0 1 0 0 1 0 2 0 1 1
0 0 0 0 0 0 0 0 1 1 0 1 0 1
0 0 0 0 0 0 0 1 2 2 1 0 4 2
0 0 0 0 0 0 0 1 2 2 1 1 2 3
M2 =
(M2)uv for uv represents the number of common neighbor of the nodes u and v.
local spectral moment
Subgraph centrality

The subgraph centrality of the node i is given by
Let λ be the main eigenvalue of the adjacency matrix A. It can be shown that
Thus, the subgraph centrality of any vertex i is bounded above by
Subgraph centrality

Table 2. Summary of results of eight real-world complex networks.