THE ARMA MODELS APPLIED TO THE FLOW OF KARSTIC SPRINGS

WATER RESOURCES BULLETINVOL. 32, NO.5 AMERICANWATER RESOURCES ASSOCIATION OCTOBER 1996

THE ARMA MODELS APPLIED TO THEFLOW OF KARSTIC SPRINGS1

Alberto Padilla, Antonio Pulido-Bosch, Maria L. Calvache, and Angela Vallejos2

ABSTRACT: Autoregressive moving average (ABMA) models havebeen applied to study the flow series of the karstic springs of LaVilla, Fuente Mayor (Spain), and Aliou (France). The theoreticalmeaning of the parameters involved in the model upon applying itto a simplified scheme of the emptying of a karstic aquifer is firstanalyzed. The types of transformations necessary to apply thesemodels to the flow series that lack normality and have strong peri-odic components are also indicated, as are the advantages of thistype of model and the physical significance of the parametersobtained, with respect to the standpoint of hydraulics, ranging fromrather homogeneous aquifers (La Villa) to extremely karstic (Aliou),including aquifers with intermediate characteristics (FuenteMayor).(KEY TERMS: ground water hydrology; ARMA model; time seriesanalysis; karstic spring; hydrograph analysis and modeling; quick-flow; baseflow.)

INTRODUCTION

The modeling of the discharge of a karstic aquiferby way of springs is a complex process. The difficultyarises from the fact that the discharge is a response tothe recharge undergone by the aquifer primarily fromrainfall. Some springs respond rapidly and clearly torainfall, while others behave with more inertia andless correspondence to the amount of precipitation.This difference in the functioning of carbonateaquifers is owed to the existence of a quickflow due tothe circulation of the water through a network ofdrains formed during the karstification process, and abaseflow due to the circulation of the water throughthe carbonate matrix and small fissures (Atkinson,1977; Bakalowicz, 1977; Drogue, 1980; Smart, 1988;Christopher, 1992). The predominance of one type offlow or the other depends on the degree of karstifica-tion in the carbonate aquifer (Padilla et al., 1994).

The ARMA models have been used to model theunivariate seasonal hydrological processes (Salaset al., 1980, 1982; Obeysekera and Salas, 1986;Haltiner and Salas, 1988; Ula, 1990). In the presentpaper we shall attempt to demonstrate the applicabil-ity of the ARMA models to a series of springs drainingcarbonate aquifers in which the quickflow and base-flow components influence the discharge of the springin markedly different ways. These univariate modelsare based on the analysis of the stochastic structureof time series, with the aim of short-term forecasting,completing data or generating synthetic series thatmaintain the mean statistics and, above all, the timecorrelation (autocorrelation function) of the originalseries.

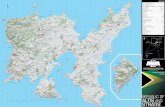
The three springs studied belong to carbonateaquifers in Spain and France (Figure 1). The spring ofLa Villa drains the karstic aquifer of El Torcal (south-ern Spain), which occupies some 28 km2 and has pre-dominantly baseflow. The spring of Aliou (FrenchPyrenees), which has a surface area of about 12 km2,is characteristic of quickflow. Finally, the spring ofFuente Mayor in the karstic aquifer of Simat deValdigna (eastern Spain), with approximately 20 km2,is an intermediate case with respect to the formertwo, having both flow components of quickflow andbaseflow. The relationship between the discharge ofeach spring and the functioning of the aquifer beingdrained has been established by classic hydrogeologi-cal methods, spectral and cross-correlation analysis,and mathematical flow models (Mangin, 1975, 1981a,1981b, 1984; Mangin and Pulido-Bosch, 1983; Padilla,1990; Pulido-Bosch and Padilla, 1990; Padilla et al.,1994).

1Paper No. 95054 of the Water Resources Bulletin. Discussions are open until April 1, 1997.2Respectively, Private Researcher, Investigaciones Geologicas y Mineras S.A. Urban, Alcázar GeniI. Ed. Zulema, Bajo, Granada, Spain;

and Professors and Research Fellow, Departamento de Geodinámica, Universidad do Granada, 18071 Granada, Spain.

917 WATER RESOURCES BULLETIN

Padilla, Pulido-Bosch, Calvache, and Vallejos

Fuente Mayor

Figure 1. Location of the Three Aquifers Studied in this Paper.

METHODOLOGY AND PHYSICALJUSTIFICATION

Here we apply an ARMA (p,q) model of constantparameter, whose general expression (Box and Jenk-ins, 1976) is

p q

Zt=> d?z1_+at— 01a1_11=1 j=1

where zt represents a standard periodic hydrologicaltime series, 4j and O are time-varying autoregressiveand moving average coefficients, respectively, and atis an independent and normally distributed variable,white noise. The number of parameters involved infitting this model would be 2+p+q (the mean, thestandard deviation, and p autoregressives and q mov-ing-average parameters).

Now, we try to justify the physical meaning whichan ARMA model can have when applied to the studyof the flows of a spring draining a karstic system. Fig-ure 2 shows a schematized karstic aquifer, where thevariables represent discretized values. We assumethat in this system the functions that link the trans-ference of volumes are linear; that is, these are invari-ants through time and do not depend upon the stateof the system. The precipitation at a given instant, Pt'is divided into the infiltration towards the saturated

WATER RESOURCES BULLETIN 918

zone flowing slowly (baseflow), aPt; the evapotranspi-ration, bPt; and the infiltration circulating rapidlythrough the conduits of high transmissivity (quick-flow), which in an isolated system will be equal to (1-a-b)Pt=dP. The parameters a, b, and d represent thedifferent fractions into which the precipitation isdivided. The flow of the spring at an instant t will begiven by

= cV1 + dP1

where cVti indicates the fraction of the stored volumein the previous instant drained by the spring. On theother hand, the stored volume at the moment t isequal to

V1 = V1 + aP1 —cV11 = (1-c) V1 + aP1

and by extension from Equations (1) and (2)

Qj = cV1 + dP11

V11 = (1-c) V2 + aP11

where V€2 is found as

- Q1_1-dP1_1Vt_2__

ALIOU SYSTEMAliou

0 1km

TORCAL DE ANTEQUERA

Ilimestone

dolostone

SIMAT SYSTEM

0 2km0 2km

The ARMA Models Applied to the Flow of Karstic Springs

which, combined this with Equation (3)

= (1—c)(Qt_i — dPi_i) +C

upon substituting V.1 in Equation (1) and operating,we finally obtain

= (1-c) + dP — [d(1-c) — cal P1

Rainfall

Figure 2. Conceptual Representation of the Discharge Processof a Karstic Spring (modified from Salas et al., 1980).

This expression is similar to that of an ARMAmodel (1,1), in which the precipitation is a randomand independent variable; (1-c) equals 4 and indi-cates the manner in which the saturated zone drainsthrough small discontinuities (baseflow); dP equalsthe random term at and represents the quickflow atthe time t; and [d(1-c)-ca] equals the term 9, whichlacks clear physical meaning, although it could be theprecipitation fraction circulating by the high trans-missivity conduits in the previous instant, in whichcase it can be considered to be representative of thedegree of organization of the karstic system (networkof conduits and channels) influenced by the precipita-tion regime.

The procedure followed in the present paper was asfollows. First, the spring flow series studied weretransformed, with the intention of reducing the biasand eliminating the periodic character of the series.Second, the autoregressive parameters and those ofthe moving-averages were calculated by applying theleast-squares method by the algorithm of Marquardt(1963). Finally, the best ARMA model was fitted tothe time series of data. A discussion of the efficiencyof the model follows.

DATA USED

For the La Villa spring the seven years of1974/1975 to 1980/1981, with sampling intervals ofthree days, were used, providing a total of 854 datapoints. From the spring of Fuente Mayor, on the otherhand, the only data available were from a flow seriesof four years (1973/1974 to 1976/1977), also with ansampling interval of three days; in this case a total of488 data points were obtained. In the Aliou spring theregister was daily over five years (1970/197 1 to1974/1975), for a total of 1825 data points.

Figure 3 presents the hydrograph of each karsticspring studied. The graphs indicate that the springsof La Villa and Aliou behave in opposite ways. In theformer, the functioning of the system is rather iner-tial, which is reflected in the gentler slopes away fromthe peaks, while in Aliou the drops after the peaksare almost instantaneous, indicating much less iner-tia. The spring of Fuente Mayor is an intermediatecase, though more similar to La Villa. Therefore, thethree-day intervals of sampling at La Villa spring donot represent a loss of information since the storage ofthese systems is greater than this time period; atAliou, however, daily data were necessary becausestorage was practically nil.

In the hydrographs of the La Villa and FuenteMayor springs, there is a strongly annual periodiccomponent. The Aliou hydrograph also shows a cer-tain periodicity due not to the high regulation of thesystem, as in La Villa or Fuente Mayor, but to themore intense peaks in the periods of high waters.Consequently, there is a direct relationship with thedistribution of the precipitation in the sector.

We have a clearly periodic flow series (Figure 3),which can be either modeled by using a periodicARMA or transformed to eliminate the periodicityand afterwards submitted to a constant-parameterARMA. This latter option has been followed in thepresent work.

DATA-SERIES TRANSFORMATION

After testing a series of transformations todecrease the bias, we chose the logarithmic as themost suitable because it provides the highestdecrease. Table 1 represents the values of the mean(m), standard deviation (s), and bias (g) of the seriesqt (untransformed flow) and the new values of theseries Yt = log(q) (after the transformation). The biasin all three cases decreased appreciably, only FuenteMayor values remaining slightly, but, as will be seenbelow, diminishing in the next transformation.



Figure 3. Flow Hydrographs of La Villa,Fuente Mayor, and Aliou.

The periodicity could have been eliminated by thetransformation

YV,T - mTZV,T =

ST

where w indicates the length of the fundamental peri-od (122 or 365); ii the mean of the series UT; and h*the number of significant harmonics (significantmeaning those periods in which either high varianceis explained or a break in the periodgram occurs). TheA and B coefficients are obtained from these expres-sions:

AJ=-—uTcos (2T) Bf=--uTsin (2JfT)

To ascertain the number of harmonics needed, theaccumulated periodgrams arranged in descending

To analyze the periodicity of the most significantstatistics (mean and standard deviation), we groupedthe terms of the series Yt in their corresponding years;this new series was represented by YV,T where Vrefers to the years and T to the intervals into whichthe year was divided (365 for Aliou and 122 for LaVilla and Fuente Mayor). For each interval, the mean(mT) and standard deviation (ST) of the number ofyears in the series (N) would be calculated by theseexpressions:200 400 600 800

TIME (Interval 3 dayI

1.5

Ew

a 1IU'

0.5

0

0.8rE— 0.6aU'

0.4

0.2

0

20

- 15

E

I

0

mT = cY1Tr

'N 2

ST = a!(YV,T

—mT)

Yv=i N

TIME (Interval 3 dayI

Aliou

ilk1 i0 400 800 1200

TIME (Interval 1 day)1600

To avoid use of an ARMA model requiring a largenumber of parameters (365 or 122 according to thecase), we estimated the mT and ST by the most signifi-cant coefficients, obtained by the Fourier transforma-tion of both statistics (Salas et al., 1980). This methodhas frequently been used by various authors, notablyChu and Katz (1989) and Wasimi (1990).

Any series, written generically UT, can be estimat-ed by Fourier transformation with the expression(Yevjevich, 1972)

h* r / /— 2fljT . 2ITIjTUT=U+ IA1cosI 1+B1sinIL w)J=1

T=1,.. .,wTABLE 1. Values of the Mean (m), Standard Deviation (s),and Bias (g) of the Series qt (untransformed flow), y

(after logarithmic transformation), and zvT(after transformation for eliminating the periodicity).

Spring Stat. qt yt zV,T

La Villa msg

0.410.2801.81

—0.47

0.260.33

0.0081.05

-0.09

Fuente Mayor msg

0.2240.1391.61

—0.7150.2270.705

0.0121.0890.230

Aliou msg

0.4670.9416.36

—0.849

0.7070.02

—0.021.130.03


j=1,2,..


order of explained variance have been obtained for mTand ST of the three springs (Figure 4). These repre-sent the percentage of variance accumulated from thefirst 10 most significant harmonics for La Villa andFuente Mayor springs and from the 40 most signifi-cant harmonics for the Aliou spring. In the case of theLa Villa spring, the first harmonic (365 days) explains95 percent of the total variance of mT; the rest of thevariance explained can be considered random. Accord-ing to the periodgram of 5T' four harmonics explain 93percent of the total variance. For Fuente Mayorspring, a higher number of harmonics is needed: threeexplain 94 percent for mT, and four explain 85 percentof the total variance. The periodgrams of the Aliouspring show that a great part of the variance of mT isexplained with few harmonics. Conversely, the 5T isextremely random, and there is no clear break in itsperiodgram for a fixed number of harmonics. Never-theless, we have considered three harmonics signifi-cant for estimation of mT, which explain 90 percent ofthe total variance, and eight harmonics for estimationof 5T percent of the total variance).

Figure 5 represents the realthT and 5T and the esti-mated mT and 5T by the Fourier transformation in the122 intervals into which we divided the year for LaVilla and Fuente Mayor springs and 365 intervals forAliou spring. In the first two cases, the adjustment isquite acceptable with the number of harmonics select-ed, the real values fluctuating at random around theestimated values. On the other hand, the Aliou seriesshows greater variation between real and estimatedvalues than does the La Villa or Fuente Mayor series.This may be due to the fact that in Aliou daily datawere taken while in La Villa and Fuente Mayor thedata interval was three days. This variation is dis-tributed evenly over the entire period, so we have toconsider it random.

Finally, the periodicity of the y series is eliminatedby this transformation:

YV,T-rnTZVT

ST

Below we will examine the series of data ZV,T totest whether the periodicity in series y has in factbeen eliminated.

The coefficient of autocorrelation Rk,T, is calculatedusing the following expression (Salas et al., 1980):

N (zv,T_k — mT_k)RK,T= , (zv,T-mT) Nv=i 5T5T-k

As shown in Figure 6, the first coefficient of auto-correlation R1,T for each of the T intervals remainsrelatively constant in turn at a value in the La Villa(0.85) and Fuente Mayor (0.75) series. In the Aliouseries, R1T shows a greater dispersion because thesampling interval is small (1 day) and, above all,because the lower inertia of the system causes sharpdecreases so that the discharge rate is not indepen-dent of the state of the aquifer (Padilla, 1990).Nonetheless, we confirmed that many of the R1,T arearound 0.8, corresponding to the period of very lowflow. The rest fluctuate randomly in a widely variablerange but always less than 0.8, without a fixed rate,and they correspond to the periods when flow is influ-enced by precipitation.

Therefore, the adjusting of a constant parameterARMA model is feasible, above all in view of the accu-mulated periodgrams of R1T, for each year that showsno significant periodicity (Figure 7).

The new statistics for the series zVT of each aquiferis shown in Table 1. The bias has in fact been reducedfor the series of Fuente Mayor spring.

Figure 4. Accumulated Periograms of Means (mT) and Standard Deviations (sT)of the Series yV,T of La Villa, Fuente Mayor, and Aliou.


100

&wU2

50Lu2

xLu

0

100

HARMONICS



0.4

0

-0.4

-0.8

TIME IJ'JTERVAL

0

F. Ma!jor

-0.4 -

-0.8 -

0 40 80TIME INTERVAL5

120

intervals of 95 percent are included, given by theexpression of Anderson (1941) (Figure 8):

±Lk(95%)=—1± L96VN—k— 1

N—k

where N is the sample size, and the partial autocor-relogram (Figure 9) with reliability limits of 95 per-cent, given by the expression of Box and Jenkins(1976):

±L(95%) =

All the graphs, especially any dealing with partialcorrelograms (Figure 9), indicate a very strong firstautoregressive parameter. In some cases, we find coef-ficients that exceed the 95 percent limit, although notin a significant way.

Therefore, the ARMA models to be adjusted in thethree cases will have one autoregressive parameter.To fix the number of parameters of moving averages,a series of tests have been carried out (Table 2).

In the case of La Villa spring, of the six modelsanalyzed, the ARMA(1,2) and ARMA(1,3) present asum of square residuals (Sa2) smaller than the rest;these can be considered equivalent. Nevertheless, thebest of these is the ARMA(1,2), the Akaike Informa-tion Criteria (AIC) being the least. The introduction ofa third parameter of moving averages does not repre-sent a significant improvement. Therefore, the defini-tive model ARMA(1,2) is expressed as

= o•8i + a1 + 0. 293a1_1 + 0. 136a1_2 —0.004.

Of the tests carried out for Fuente Mayor spring,the ARMA(1,0) shows a lower value for AIC, and therest of these show no decrease of Sa2, despite theincreased number of parameters. The modelARMA(1,0) is expressed as

£1=0.89211_1+a1—0.011

Of the five models analyzed in Aliou, theARMA(1,2) presents the least AIC value, with a con-siderable reduction of Sa2 and Q, compared to thosewith a lesser number of parameters. The modelARMA(1,3) is equivalent, but its AIC is neverthelessgreater and shows no appreciable improvement overARMA(1,2). The adjusted model is represented by theexpression

= O.811_i +a1 +0.071a1_1—0. 119a1_2 —0.003.

0 100 200TIME INTER VALE

1.2

0.8

0.4

0

-0.4

-0.8

-1.2

-1.6

-2.0300 400

Figure 5. Values of , and mt, s of the SeriesYV,T of La Villa, Fuente Mayor, and Aliou.

ADJUSTMENT OF THE MODELS

The adjustment of the models will be done over theseries of seven, four, and five years of zt (obtainedfrom zV,T) of each spring studied.

To obtain the autoregressive parameters and, to alesser extent, the moving averages that the ARMAmodels applied to each spring should have, we carriedout the autocorrelograms of; in which the confidence


0 40 80TIME INTERVALS

120 0 100 200 300 400TIME INTERVALS

'..'%%V,__

0.5-

0-

-0.5-

La Villa

0.5

RIT -

0

-0.5

F. Major

120 0 4080TIME INTERVALS

0.5-.-

. — ...- -S

RIT .-

0- .-

-0.5

Allou

ElU2

0LU

2

C.xEl

FigureS. First Autocorrelation Coefficient (R1,T) of the Series zvT of La Villa, Fuente Mayor, and Aliou.

100

50

0600

ElU2

0LU

2

0.xEl

20HARMONICS

40 0 20 40HARMONICS

60

Figure 7. Accumulated Periodgrams of Rl,T of the Series zvT of La Villa, Fuente Mayor, and Aliou.

0 40 80 120 160HARMONICS

o 5

\\

___LaVIlla

—L 95%

R

0.5

R

0

AIIou

--L95%

20 40K

40K

-0.520 40 60

K

Figure 8. Autocorrelograms of the Tipified Series z of the Flow at La Villa, Fuente Mayor, and Aliou.



Figure 9. Partial Autocorrelograms of the Series zt of the Flow at La Villa, Fuente Mayor, and Aliou.

TABLE 2. Parameters of the Adjusted Models to z Series at La Villa, Fuento Mayor, and Aliou. C. constant;autoregressive coefficients; 0, moving average coefficients; Sa2, sum of square residuals; x2 for the

first 20 autocorrelation coefficients; AIC, information criterion of Akaike (1974) of parsimony.

Model C 41 2 2 03 Se2 Q AIC

La Villa

ARMA(1,0) —0.002 0.966 — — — — 65.1 93.9 —2196

ARMA(1,1) —0.004 0.955 — —0.245 — — 61.0 36.6 —2249

ARMA(1,2) —0.004 0.938 — —0.293 —0.136 — 60.1 24.9 —2260

ARMA(1,3) —0.004 0.944 — —0.278 —0.117 —0.073 60.0 23.9 —2259ARMA(2.0) —0.002 1.207 -0.251 — — — 60.5 28.7 —2256ARMA(2,1) —0.003 1.228 —0.270 0.005 — — 60.5 28.8 —2256

Fuente Mayor

ARMA(1,0) —0.011 0.892 — — — — 117.7 15.6 —413

ARMA(1,1) —0.016 0.900 — —0.029 — — 117.6 15.6 -411ABMA(2,0) —0.016 0.872 0.024 — — — 117.6 15.6 —411

ARMA(2,1) —0.030 0.143 0.673 —0.754 — — 117.6 15.6 —409

AliouARMA(1,0) 0.001 0.798 — — — — 848.4 46.4 —1396ARMA(1,1) —0.002 0.744 — 0.149 — — 839.2 27.3 —1414ARMA(1,2) —0.003 0.811 — —0.071 0.119 — 832.9 16.3 —1425

ARMA(1,3) —0.006 0.822 — —0.049 —0.119 —0.008 832.4 25.5 —1424ARMA(2,0) —0.011 0.862 —0.077 — — — 840.4 25.5 —1411

EFFICIENCY OF THE MODELS

One way of testing the efficiency of the adjustedmodels in each case is by proving the independence ofthe residuals. For this we used the test of Porte Man-teau using the value of Q. The statistical Q is equiva-lent to the value of2 for the first L coefficients of theautocorrelation function of the Rk(a) residuals, and itsvalue is given by


L

Q=N> R(a)k= 1

If Q < 2 with L-p-q degrees of freedom, then theindependence hypothesis is accepted.

Table 3 shows the parameters necessary for apply-ing the Porte Manteau test to the residuals of thethree ABMA models applied. In the three cases, theindependence hypothesis of the residuals is accepted.

0.5

F. Mayor

0•L 95%

—L 95%

0 2 4 6 8 10

K12 14 2 4 6 8

K


TABLE 3. Parameters for Applying the Porte Manteao Test.

Spring Q x2

La VIlla 24.9 27.6

Fuente Mayor 15.62 30.1

Aliou 16.26 27.6

Similarly, the autocorrelograms of the residuals forthe first 50 coefficients (Figure 10) show that hardlyany fall outside the 95 percent reliability limits, con-firming the independence of these coefficients. Thepresence of certain coefficients that exceed the 95 per-cent limit, being an isolated phenomenon and notappearing in the first terms of the autocorrelogram,do not lead us to consider a possible ARMA modelwith moving average coefficients.

Upon confirming the independence of the residuals,we arranged the synthetic series of which would

have 854, 488, or 1825 data, depending on whetherthe spring used was La Villa, Fuente Mayor, or Aliou,respectively. The random values were generated withthe same average and standard deviation, followingthe same distribution as shown by the residuals of themodels selected. This distribution can be seen in thehistograms of the residuals for each model adjusted(Figure 11). In La Villa and Fuente Mayor, there is anormal distribution N(0,0.27) and N(0,0.49), respec-tively. In Aliou, on the other hand, the distribution islognormal of three parameters ( = -1.6, j.t = 0.49 and

= 0.36).The high resemblance between the partial correlo-

grams (at least in the first coefficients) of the synthet-ic series t and the real one z (Figure 12) indicatesthat the model selected preserves the principal coeffi-cients of autocorrelation from the original series,which was an aim for the ARMA models.

To obtain the series of synthetic spring flows,we have followed the inverse process, carrying out

Figure 10. Residual Autocorrelograms of the ARMA Model Adjusted to theSeries z of La Villa, Fuente Mayor, and Aliou.

Figure 11. Histograms of the Residuals Obtained on Adjusting the ARMA Modelsto the Series z of La Villa, Fuente Mayor, and Aliou.

0

-0.5

•La Villa F. Mayor

0.5

R

0,5

R

-

-L 95%-I. 95%

20K

40 0

Aljc,u

.195%,'-. A-195%

',

20 K 40 00

U 0.2UI

aU-

a0.1I-

a

20K

40

UUI

0aU.aI-1a

0.3

0.2

0.1

0

-1.8 0 1.8 -0.96 0INTERVALS INTERVALS

0.96 -1.6 0INTERVALS



transformations of the series. Once values weregrouped according to years, the V,T was transformedby these expressions

Yv,T = STZV,T + rnT

qv, =

varying the values of V and T according to the yearsand the data of each case studied.

Synthetic hydrographs, in morphology, quite closelyresemble real hydrographs (Figure 13). In the case ofFuente Mayor, we find a more accentuated componentof white noise, possibly due to the absence of moving-average coefficients that would have softened thisnoise. However, the introduction of a greater numberof coefficients does not represent an improvement.

The correlograms of the series and q (Figure 14)are very similar. In the La Villa and Fuente Mayorcases, this similarity is especially evident in the firstcoefficients. However, the periodic component of ismore regular than the real one due to the estimationsof the means and standard deviations obtainedthrough transformation of the data by the coefficientsof the most significant harmonics.

FINAL DISCUSSION

With the results obtained from adjusting theARMA models to the flow of the three karstic springs,we have been able to make the following observations.

Autoregressive coefficients can be representative ofthe recession coefficient (Ford and Willians, 1989;LaMoreaux, 1993), in the strictest sense of the term —


that is, the speed of the empty of the saturated zonewithout the influence of precipitation (baseflow). Onthe other hand, such a high value cannot be explainedat Aliou, where the storage as a whole is very low.Nevertheless, the reduced saturated zone can providea small amount of storage, although it has very littlerelative importance in the flow at Aliou. The highautoregressive coefficient obtained would correspondto its depletion.

Consequently, to have a general perspective on themodel, we must take into account the moving-averagecoefficients and the residual variance, since both indi-cate the weight of the randomness in the system.Thus, at Aliou, the first moving-average coefficient issubstantially higher (-0.071 as against -.293) and thevariance almost seven times greater than the corre-sponding values at La Villa. Even taking into accountthat the sampling interval of the series is different(three days at La Villa and Fuente Mayor and one atAliou), we find that the random part of the model hasmuch greater relevance in the system at Aliou. Weinterpret these parameters as being representative ofthe extent of karstic organization of the system (pres-ence of karstic channels, quickflow).

The absence of significant moving-average coeffi-cients in the model adjusted for the flow at FuenteMayor is difficult to explain, given that the randomcomponent must be more important since the karsticcharacteristics are more highly developed than at LaVilla, where moving-average terms nevertheless exist.The variance of the residuals, however, is thereforemuch lower, at Fuente Mayor. The explanation mightbe that the low randomness of La Villa shows greaterstorage, permitting representative coefficients to existoutside the three-day interval (the moving-averagecoefficients refer in some way to the residual correla-tion between intervals). At Fuente Mayor, the rather

0.5 0.5

0

-0.5

0

—L 95%

0 2 4 6 5 10 12 14

K

Figure 12. Partial Autocorrelograms of the Series and z of La Villa, Fuente Mayor, and Aliou.

0 2 4 6 8 10 12 14

K

-0.5

K

! 1.5E

a

I0.5

0

r15

Ea

10(IUis



2 1.

0.5

Ro

-0.5

—1

200 400 600 800TIME (interval 3 days)

La Villa

0 40 80 120 160 200 240K

rE

0.5

0

0.5

Ro

100

20

-0.5

200 300 400

TIME (Interval 3 days)500

0 40 80 120 160 00 240

K

0.5

R

0

-0.5

AIlou

0 400 800 1200 1600TIME (interval 1 day)

0

Figure 13. Synthetic Hydrographs Obtained with the ModelAdjusted to the Flow at La Villa, Fuente Mayor, and Aliou.

high randomness of the series, shown by residualvariance, does not correlate with the previous residu-als; that is, the randomness is concentrated in theterm at of the model. This explanation seems to con-firm that given by Mangin and Pulido-Bosch (1983)that a "rapid circulation" is detected due to massivereleases from the poljes (karstic flat-floored depres-sions) drained by ponors (shallow-holes or streamsinks).

We should point out also that the usefulness of theARMA models is rooted in the generation of the syn-thetic series conserving the mean statistics, especiallythose referring to the autocorrelation function, withthe aim of using it in other types of models and com-pleting series of data.

0 100 200 300 400 500K

Figure 14. Autocorrelograms of the Real Flow (q) and theGenerated () at La Villa, Fuente Mayor, and Aliou.

ACKNOWLEDGNENTS

We are grateful to Dr. A. Mangin for help with the data relatedto the spring at Aliou and for his helpful comments on thesemanuscripts. The research for this project was financed by CICYT(Project AMB92-0211).

LITERATURE CiTED

Atkinson, T. C., 1977. Diffuse Flow and Conduit Flow in LimestoneTerrain in the Mendip Hills, Somerset (Great Britain). Journalof Hydrology 35:93-100.

Anderson, R. H., 1941. Distribution of the Serial Correlation Coeffi-cients. Ann. Math. Statist. 8(1):1-13.

Bakalowicz, M., 1977. Etude du degre d'organisation des ecoule-ments souterraines dans les aqui!res carbonates par une méth-ode hydrogeochemique nouvelle. Comptes Rendues del'Académie des Sciences de Paris 284:2463-2466.

Box, G. E. P. and G. M. Jenkins, 1976. Time Series Analysis: Fore-casting and Control. Holden Day, San Francisco, 575 pp.


Christopher, G. G., 1992. Geochemical and Kinetic Evolution of aKarst Flow System: Laurel Creek, West Virginia. Ground Water30(2): 187-198.

Chu, P. S. and W. Katz, 1989. Spectral Estimation Time SeriesModels with Relevance to the Southern Oscillation. Journal ofClimate, American Meteorological Society 2(1):86-90.

Drogue, C., 1980. Essai didentification d'un type de structure demagasins carbonates fissures. Application a linterpretation decertains aspects du fonctionnement hydrogeologique. Memoireshors Série de la Societe Geologique de France 11:101-108.

Ford, D. C. and P. W. Willians, 1989. Karst Geomorphology andHydrology. Unwin Hyman, 601 pp.

Haltiner, J. P. and J.D. Salas, 1988. Development and Testing of aMultivariate Seasonal ARMA (1,1) Model. Journal of Hydrology104:247-272.

LaMoreaux, P. E., 1993. Annotated Bibliography of Karst Terranes,IAII, 14, Verlag Heinz Heise, 425pp.

Mangin, A., 1975. Contribution a l'étude hydrodynamique desaquifbres karstiques. Lab. Sout. du C.N.R.S. (Moulis). Ph.D.Thesis, University of Dijon. In: Annales Spéléologie 29(3):283-332; 29(4):495-601; 30(1):21-124.

Mangin, A., 1981a. Utilisation des analyses correlatoire et spectraledans systémes hydrologiques. Comptes Rendues de l'Académiedes Sciences de Paris 293:401-404.

Mangin, A., 1981b. Utilisation des analyses corrélatoire et spectralecroisées dans la connaissance des systèmes hydrologiques.Comptes Rendues de l'Academie des Sciences de Paris 293:1011-1414.

Mangin, A., 1984. Pour une meillure connaissance des systemeshydrologiques a partir des analyses correlatoire et spectrale.Journal of Hydrology 67:25-43.

Mangin, A. and A. Pulido.Bosch, 1983. Aplicacion de los análisis decorrelación y espectral en el estudio de los acufferos kérsticos.Tecniterrae 51: 53-65.

Marquardt, D. W., 1963. An Algorithm for Least Squares Estima-tion of Non Linear Parameters. J. Soc. md. App. Math. 2:43 1-441.

Obeysekera, J. T. B. and J. D. Salas, 1986. Modeling of AggregatedHydrologic Time Series. Journal of Hydrology 86:197-219.

Padilla, A. 1990. Los modelos matemáticos aplicados al estudio delos acufferos kársticos. Ph.D. Thesis, Universidad of Granada,267 pp.

Padilla, A., A. Pulido-Bosch, and A. Mangin, 1994. Relative Impor-tance of Baseflow and Quickflow from Hydrographs of KarstSpring. Ground Water 32(2):267-277.

Pulido-Bosch, A. and A. Padilla, 1990. Evaluation des resourceshydriques de l'aquifbre karstique du Torcal de Antequera (Mála-ga, Espagne). Hidrogeologfa 5:11-22.

Salas, J. D., V. Yevjevich, and W. L. Lane, 1980. Applied Modelingof Hydrologic Time Series. Water Resources Pub. Littleton, 484pp.

Salas, J. D., D. C. Boes, and R. A. Smith, 1982. Estimation ofARMA Models with Seasonal Parameters. Water ResourcesResearch 18(4):1006.1010.

Smart, C. C., 1988. Artificial Tracer Techniques for the Determina-tion of the Structure of Conduit Aquifers. Ground Water 26(4):445-453.

Ula, T. A., 1990. Periodic Covariance Stationarity of MultivariatePeriodic Autoregressive Moving Average Processes. WaterResources Research 26(5):855-861.

Wasimi, S. A., 1990. A Hybrid Model for Forecasting Daily Rainfall.Water Resources Research 26(11):2741-2746.

Yevjevich, V., 1972. Stochastic Processes in Hydrology. WaterResources Pub., Fort Collins, Colorado, 276 pp.


THE ARMA MODELS APPLIED TO THE FLOW OF KARSTIC SPRINGS

Documents

Transcript of THE ARMA MODELS APPLIED TO THE FLOW OF KARSTIC SPRINGS