Neurons – Fundamental units of computationlabs.seas.wustl.edu/bme/raman/Lectures/Lecture2_HH.pdf3!...
Transcript of Neurons – Fundamental units of computationlabs.seas.wustl.edu/bme/raman/Lectures/Lecture2_HH.pdf3!...

1!

2!
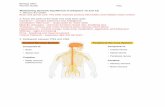
Neurons – Fundamental units of computation!

3!
Resting Membrane Potential!g Difference in voltage between the interior and
exterior of a neuron!
!
g Three main players!n Salty fluids on either side of the membrane"n The membrane itself"n Proteins that span the membrane"
Intracellular!
Extracellular!

4!
Typical Ionic Concentrations!

5!
Movements of ions - Diffusion!
Membrane impermeable to the ions
Na+ cation Cl- anion

6!
Movements of ions – Electric Field!Na+ cation Cl- anion
Cathode Anode

7!
Establishing equilibrium!
A net accumulation of positive charge on the outside and negative charge on the inside retards movement of K+
An equilibrium is established such that there is no movement of ions and there is a charge difference
Neuroscience, Bear et al. 3rd edition
Diffusion causes Potassium ions to move from region of higher concentration (intracellular side) to a region of lower
concentration (extracellular side)

8!
Reversal potential!g Nernst Equation!
Reversal potential at 25C ENA = 55mV EK = -77 mV ECL = -61 mV
!
Eion =RTzFln [ionout ][ionin ]
[ionin ], [ionout] are ionic concentration inside and outside the cell T is temperature (Kelvins) R is gas constant z is the valence of the ion F is Faraday’s constant: it is the magnitude of electric charge per mole of electrons

9!
Resting membrane potential!g Goldman Hodgkin and Katz equation!
!
ENa,K,Cl =RTFlnPK [Kout ] + PNa[Naout ] + PCl[Clin ]PK [Kin ] + PNa[Nain ] + PCl[Clout ]
Typical resting membrane potential Vrest = -65 mV

10!
Some terminology!g Depolarization!
n Change in cellʼs membrane potential making the inside of the cell more positive (or less negative) with respect to the cellʼs outside "
g Hyper-polarization!n Change in cellʼs membrane potential making the inside of the
cell more negative (or less positive) with respect to the cellʼs outside"
g Inward current (example due to Na+ ions)!n Flowing into the cell (considered negative)"
g Outward current (example due to K+ ions)!n Flowing out of the cell (considered positive)"
g Action potential, Spike!n An “all or nothing” event during which the membrane potential
rapidly rises and for a brief moment Vinside-Voutside is positive"

11!
Action Potential!
0 mV
EK
ENa
Potassium Channels are opened

12!
Action Potential!
0 mV
EK
ENa
Sodium Channels are opened

13!
Action Potential!
0 mV
EK
ENa
Open Sodium Channels
-65 mV
Close Na Channels
Open K Channels

14!
Action Potential!
Neuroscience, Bear et al. 3rd edition

15!
Action Potential!
Neuroscience, Bear et al. 3rd edition

16!
Action Potential!
Neuroscience, Bear et al. 3rd edition

17!
Membrane Current and Conductance!g Net movements of ion will cause ionic
current Iion!
g The number of ion channels open will be proportional to an electrical conductance (gk, gNa; inverse of resistance)!
g Ionic current will flow only as long as membrane potential Vm is not equal to reversal potential Eion!
! ! !Iion = gion (Vm-Eion)!

18!
Refractory Period!
[From web]

19!
Electrical Circuit of a Patch of neuron!
[Notes borrowed from Araneda]

20!
Passive properties of a Neuron!
[Notes borrowed from Araneda]

21!
Passive properties of a Neuron!
[Notes borrowed from Araneda]

22!
Passive properties of a Neuron!
[Notes borrowed from Araneda]

23!
Electrical Circuits with R and C elements!
[Notes borrowed from Araneda]

24!
Electrical Structure of Small Passive Neuron!
Many Small RC circuits Since the cell is so small we can assume same membrane potential everywhere (isopotential)
A battery to account for resting membrane potential
Resistor mimics ion channel
[Koch, 1999]

25!
Membrane Patch Equation!
!g Show that the
solution is:!
I inj R C
!
Iinj = C dVm (t)dt
+Vm (t)R
Injected current = Capacitive current + Resistive current
!
Vm (t) =V"(1# e# t$ )
at t = 0 V = 0$ = RC V" = IinjR

26!
RC Circuit!

27!
Equivalent circuit!
Current is carried through the membrane either by charging the membrane capacitor or by movement of ions through the resistances in parallel with the capacitor.

28!
Currents!
Total current = Capacitive current + Ionic current
Ionic current = Sodium-Current + Pottasium-Current + Leakage Current (Cl- and other ions)

29!
Ionic currents!
ENa, Ek and El are equilibrium or reversal potential for respective ion species gNa, gk and gl are ionic conductances
⎭⎬⎫
⎩⎨⎧
>
<
−−
−−
negativeisIEEpositiveisIEE
typeiontypeion
typeiontypeionNotice
Larger E-Eion the larger the current due to that ionic species

30!
Squid Axon Experiments!

31!
Voltage Clamp Technique!

32!
Hodgkin Huxley Experiments!

33!
Voltage Clamp!

34!
Measuring individual ionic currents !

35!
Voltage Clamp!
Inward current become smaller as Clamp voltage gets close to Na Reversal Potential (+55mV) and flips sign for larger depolarizations
Outward current is monotonic
as you move
away from K reversal Potential (-77mV)
!
Eion =RTzFln [ionout ][ionin ]

36!
Voltage Clamp (continued …)!

37!
Measuring individual ionic currents !g Selective measurement of the K ion flow alone is
possible by utilizing a voltage clamp step corresponding to the Na Nernst potential. !

38!
Pharmacological agents!
Puffer fish
Lips and tongue tingles, hands feel numb and trouble making movements Tetrodotoxin (TTX) – blocks voltage-gated Na channels

39!
Pharmacological agents!
Scorpion toxin
Scorpion toxin blocks voltage-gated K channels Another popular blocker is tetraethylammonium (TEA)

40!
Hodgkin Huxley!g One of the most important contributions of
Hodgkin and Huxley was their detailed discussion of membrane kinetics!
g The model was not formulated from fundamental principles but rather from theoretical insights and curve fitting !

41!
Dynamics of K Conductance (3)!
How do K conductance change with V?
Becomes more rapid at higher depolarization
Does K conductance ever return back to baseline?
No!

42!
K conductance!
Depolarization to 25 mV Repolarization back to Resting potential
Inflexion of the curve

43!
Whatʼs the best fit?!
0 5 10 15 20 25 30 35 4000.10.20.30.40.50.60.70.80.9
1
Time (ms)
GK N
orma
lized
(mS)
1-exp(-t/τ)!
[1-exp(-t/τ)]4![1-exp(-t/τ)]2!
[1-exp(-t/τ)]3!

44!
Why n4?!

45!
g Hodgkin-Huxley assumed that there is only one variable that determines the dynamics of potassium conductance!
g What does n4 represent?!n That K ions cross membrane only when four particles occupy
a certain region of the membrane"
is a constant
Dynamics of K conductance (1)!
Kg

46!
Dynamics of K conductance (1)!
www.bem.fi/book/04/04.htm!

47!
Dynamics of K Conductance (2)!
!!n αn represents of transfer from outside to inside"n βn represents of transfer from inside to outside "
g The solution of this first order ODE that satisfies the boundary condition n=n0 at t=0 is:!
!
n = n" # n" # n0( ) exp#t$n
%
& '
(
) *
!
n" =#n
#n + $n
n0 =#0
#0 + $0
% n =1
#n + $n
HW Pblm

48!
Dynamics of K Conductance (3)!
!
n = n" # n" # n0( ) exp#t$n
%
& '
(
) *

49!
Rate constants αn, βn(6)!
depolarized! hyperpolarized!

50!
Dynamics of Na Conductance (5)!
How does Na conductance change with V?
Becomes more rapid at higher depolarization
Does Na conductance ever return back to baseline?
Yes!
Are the rising and falling portions of the curves similar?
No!

51!
Dynamics of Na Conductance (1)!g Hodgkin-Huxley assumed that there are two
variables that determine the dynamics of sodium conductance!
g What does m3h represent?!n That sodium conductance is proportional to the number of
sites on the inside of the membrane which are occupied simultaneously by three activating molecules (m3) and not blocked by an inactivating molecule (m3h)."
Nag is a constant m represents the proportion of activating molecules on the inside h represents the proportion of inactivating molecules on the outside

52!
Dynamics of Na Conductance (1)!
www.bem.fi/book/04/04.htm!

53!
Dynamics of Na Conductance (2)!g The two variables obey the following first
order differential equation!
g αm or βh represents of transfer from outside to inside!
g βm or αh represents of transfer from inside to outside !

54!
Dynamics of Na Conductance (3)!g Solving the first order differential equation!
g At t=0; m =m0, h =h0!

55!
Dynamics of Na Conductance (4)!g HH noted that in resting state, sodium
conductance is negligble, so we can neglect m0, and inactivation in nearly complete if V< -30mV and hα can also be neglected!
!! is the value of sodium conductance if h
remained in its resting level h0!!
where

56!
Dynamics of Na Conductance (5)!

57!
Rate constants αm, βm(6)!

58!
How does activation variable m change with V?(7)!

59!
Rate constants αh, βh(8)!

60!
How does activation variable h change with V?(9)!

61!
Putting pieces together – HH model!

62!
Time courses of HH variables!

63!
Refractory Period!

64!
HH model - Summary!g Models a patch of membrane!g Assumes isopotential i.e. the membrane
potential is constant across the patch!g The number of channels is large enough that
individual gating events are averaged out and the Na and K currents are smooth population currents!
g The channels are not arranged in anyway which allows local interaction among small number of channels!

65!
Reducing HH models!g State variables of HH eqns : [V, m, n, h]!g Most reduction rely on two simplifications!
n Time constants are very different"n m changes so fast compared to n and h that you donʼt
need a ODE to describe it (removes one ODE)"n n+h is almost a constant; so we can eliminate one
more variable"n Now the reduced HH will have state variable [V, w]; V
– fast variable (membrane potential) and w – slow variable (potassium activation)"

66!
Reducing HH models(2)!
Original
Reduced

67!
Reducing HH models(3)!

68!
Linear Cable Equation!

69!
Action Potential Propagation!
cm!rm!
Vrest!
Ve=0!
Vm!
im =Vm !Vrest
rm+ cm
dVmdt
Transmembrane current across unit length of the axon!
im – Transmembrane current per unit length (A/cm)!rm – membrane resistance per unit length (Ωcm)!cm –membrane capacitance per unit length (F/cm) !!!

70!
Action Potential Propagation!
Transmembrane current across Δx units of the axon!
ra Δx!Ii(x,t)!Ii(x-Δx,t)!
im!
Δx!
im! im! im! im!
= unit transmembrane current (im ) times Δx!
The total membrane resistance in a fiber of length Δx is: rm/Δx!
x+Δx!x!
The total membrane capacitance in a fiber of length Δx is: cmΔx!
rm/Δx
Vrest!
c mΔ
x

71!
Action Potential Propagation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm/Δx
Vrest!
Ve=0!
Vm(x+Δx,t)!Vm(x-Δx,t)!
Ra - intracellular resistivity (Ωcm) !!Rm - specific membrane resistance (Ωcm2) !!Cm - specific membrane capacitance (F/cm2) !!
ra Δx!
Δx!ra =
4Ra!d 2
! / cm
rm =Rm!d
!"cm
cm =Cm !!d F / cm
cmΔx

72!
Action Potential Propagation!
…! …!
Note: Constant Ve is an assumption!
Plug membrane together: get linear cable!
Vm(x,t)!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!raΔx!
rm/Δx cmΔx

73!
Action Potential Propagation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
Vrest!
ra Δx! Vm(x+Δx,t)!Vm(x-Δx,t)!
imΔx!
ii(x,t)!
lim it !x = 0 =Vm x, t( )"Vm x +!x, t( )
!x=
!Vm!x
(x, t) = "ra # Ii (x, t)
Vm (x, t)!Vm (x +"x, t) = ra # "x # ii (x, t)
cmΔx
Eqn 1!
rm/Δx

74!
Action Potential Propagation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!ra Δx! Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
limit"x = 0 #$Ii$x(x,t) = im (x, t)
im (x, t)!x + Ii (x, t)" Ii (x "!x, t) = 0
Eqn 2!
By applying Krichhoffʼs current law at node x!
Ii(x-Δx,t)!
imΔx!

75!
Linear Cable Equation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!raΔx! Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
lim it !x = 0 "!Ii!x(x, t) = im (x, t)
!
limit"x = 0 #Vm
#x(x,t) = $ra % Ii(x, t)
!
1ra
" 2Vm (x, t)"x 2
(x,t) = im (x, t)Substitute!
imΔx!

76!
Linear Cable Equation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
raΔx! Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
1ra
" 2Vm (x, t)"x 2
=Vm (x, t) #Vrest
rm+ cm
"Vm (x,t)"t
If electrical nature of the membrane is constant, then!
imΔx!

77!
Linear Cable Equation!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
raΔx! Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
"2# 2Vm (x, t)
#x 2=Vm (x, t) $Vrest +%m
#Vm (x,t)#t
" = (rm /ra )%m = rmcm
Multiplying both sides by rm we get:!
λ – steady state space constant !τ -Membrane time constant!
imΔx!

78!
Space and Time constants!
g Space constant increases with square root of the axon radius!
g Time constant does not depend on axon size!!
"m = rmcm =Rm
2#a$ Cm2#a = RmCm
!
" = rm ri =
Rm
2#aRi
#a2= Rma
2Ri

79!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
raΔx! Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
"2# 2Vm (x, t)
#x 2=Vm (x, t) $Vrest +%m
#Vm (x,t)#t
" = (rm /ra )%m = rmcm
At steady state !this term = 0!
!
"2d2V (x)dx 2
=V (x) (V =Vm #Vrest )
imΔx!

80!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!Iinj(x,t)!
raΔx!
imΔx!
im (x, t) =Vm (x, t)!Vrest
rm+ cm
!Vm (x, t)!t
! Iinj (x, t)
!
1ra
" 2Vm (x, t)"x 2
(x,t) = im (x, t)

81!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!Iinj(x,t)!
raΔx!
imΔx!
1ra
! 2Vm (x, t)!x2
(x, t) = im (x, t)
1ra
! 2Vm (x, t)!x2
(x, t) = Vm (x, t)!Vrestrm
+ cm!Vm (x, t)
!t! Iinj (x, t)

82!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
! 2d 2V (x)dx2
=V (x)! rmIinj (x, t) (V =Vm !Vrest )
Iinj(x,t)!
raΔx!
imΔx!
1ra
! 2Vm (x, t)!x2
(x, t) = Vm (x, t)!Vrestrm
+ cm!Vm (x, t)
!t! Iinj (x, t)
At steady state !

83!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
Iinj(x,t)!
a general solution to this ODE for constant current applied at x!
!
V (x) = Aexp(x /") + Bexp(#x /")
A and B are constants will depend on the boundary conditions!
raΔx!
imΔx!

84!
Steady-State Solutions!
…! …!
Plug membrane together: get linear cable!
Vm(x,t)!
rm!
Vrest!
Vm(x+Δx,t)!Vm(x-Δx,t)!Ii(x,t)!
!
"2d2V (x)#x 2
=V (x) $ rmIinj (x)
Iinj(x)!
For boundary-value solutions it is often convenient to use another pair of solutions to the second-order ordinary differential equation!
!
V (x) = Aexp(x /") + Bexp(#x /")
V (x) = Acosh(x / !)+Bsinh(x / !)
!
cosh(x) =exp(x) + exp("x)
2
sinh(x) =exp(x) " exp("x)
2
raΔx!
imΔx!

85!
Case 1: Infinite Cable!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
!
V (x) = Aexp(x /") + Bexp(#x /")
For the case in which the cable extends from -∞ to +∞ we require V (-∞) = V (∞) = 0. What should be values of A and B to obey this boundary conditions? !
For x > 0; A = 0 and B = V0 (where V0 is the membrane voltage at the site of current injection)!Similarly for x<0; A = V0 and B = 0!
!
V (x) =V0 exp(" x /#)

86!
Case 2: Sealed End Cable!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
The idea for sealed end is that current should not flow across a boundary at length x = l!
V (x) = Acosh(x / !)+Bsinh(x / !)
!
dVdx x=0
= "raIinj
dVdx x= l
= 0
V (x) = Acosh(x / !)+Bsinh(x / !)
!
dV (x)dx
=A"sinh(x /") +
B"cosh(x /")
!
At x = 0 "raIinj =B#
B = "raIinj#
At x = l !0 = Asinh(l / !)+Bcosh(l / !)
A = !Bcoth(l / !)A = raIinj! coth(l / !)

87!
Case 2: Sealed End Cable!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
The idea for sealed end is that current should not flow across a boundary at length x = l!
V (x) = Acosh(x / !)+Bsinh(x / !)
!
dVdx x=0
= "raIinj
dVdx x= l
= 0
V (x) = Acosh(x / !)+Bsinh(x / !)!
B = "raIinj#
!
A = raIinj"coth(l /")
V (x) = raIinj![coth(l / !)cosh(x / !)! sinh(x / !)]
V (x) =raIinj!
sinh(l / !)[cosh(l / !)cosh(x / !)! sinh(l / !)sinh(x / !)]

88!
Case 2: Sealed End Cable!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
The idea for sealed end is that current should not flow across a boundary at length x = l!!
V (x) = Acosh(x /") + Bsinh(#x /")
!
dVdx x=0
= "raIinj
dVdx x= l
= 0
!
V (x) = Acosh(x /") + Bsinh(#x /")!
B = "raIinj#
!
A = raIinj"coth(l /")
V (x) = raIinj![coth(l / !)cosh(x / !)! sinh(x / !)]
V (x) = Vm (0)cosh[(l ! x) / !]cosh(l / !)
0 " x " l sealed x = lVm (0) = raIinj! coth(l / !)

89!
Case 3: Killed End Cable!
!
"2d2V (x)dx 2
=V (x) # rmIinj (x)
The idea here is that one of a boundaries is clamped to resting membrane potential!!
V (x) = Acosh(x /") + Bsinh(#x /")
!
dVdx x=0
= "raIinj
V (l) = 0
V (x) = Vm (0)sinh[(l ! x) / !]sinh(l / !)
0 " x " l killed end x = l
Vm (0) = raIinj! tanh(l / !)

90!
Cable Equation Solutions!

91!
Propagation of AP along an axon!

92!
Saltatory Conduction!

93!
Saltatory conduction in myelinated axons!
The Physiology of Excitable Cells. Cambridge: Cambridge Univ. Press, 1971!!