Lecture 3 addaptive huffman

October 25, 2015 1 [email protected]


Contents

Introduction

Weight the nodes

sibling property

Tree manipulation

Adaptive Huffman coding

Example 1

Decoding Procedure

Example 2


Huffman coding requires knowledge of the probabilities of the source

sequence. If this knowledge is not available, Huffman coding becomes a

two-pass procedure: the statistics are collected in the first pass, and the

source is encoded in the second pass.

In order to convert this algorithm into a one-pass procedure, Faller and

Gallagher independently developed adaptive algorithms to construct the

Huffman code based on the statistics of the symbols already encountered.

These were later improved by Knuth and Vitter.

Introduction

October 25, 2015 [email protected] 4

The Huffman code can be described in terms of a binary tree

In order to describe how the adaptive Huffman code works, we add two

other parameters to the binary tree: the weight of each leaf, which is

written as a number inside the node, and a node number.

The weight of each external node is simply the number of times the

symbol corresponding to the leaf has been encountered. The weight of

each internal node is the sum of the weights of its offspring.


Weight the Nodes

• a : 5, b: 2, c : 1, d : 3


If we have an alphabet of size n, then the 2n −1internal and external nodes

can be numbered as y1, . . . , y2n−1 such that if xj is the weight of node yj, we

have x1≤x2≤· · · ≤x2n−1.

Furthermore, the nodes y2j−1 and y2j are offspring of the same parent node,

or siblings, for 1 ≤j < n, and the node number for the parent node is greater

than y2j−1 and y2j. These last two characteristics are called the sibling

property, and any tree that possesses this property is a Huffman tree

• a : 5, b: 2, c : 1, d : 3

Sibling Property


One definition is needed to fully explain the principle of the algorithm:

Binary coding tree has a sibling property if each node (except the root)

has a sibling and if the nodes can be listed in order of non increasing

weight with each node adjacent to its sibling.

Gallager proved that a binary prefix code is a Huffman code if and only if

the code tree has the sibling property. So, algorithm modifies coding tree

each time a new symbol is encoded or decoded and whenever it detects

violation of sibling property, the tree is transformed (in order to satisfy the

sibling property again).


There are two main possibilities how to build the coding tree at the

beginning of coding:

o The tree is initialized with all symbols of input alphabet - in such

case the tree initially consists of all symbols with a chosen probability.

o The tree is initialized with ZERO node - tree initially consists of a

single node ZERO. When the encoder encounters a symbol which has

not been read yet, it writes code of node ZERO to the output followed

by the read symbol. ZERO node is then split into another ZERO node

and a node containing the new symbol.


The tree is manipulated as the file is read to maintain the following

properties:

Each node has a sibling

Node's with higher weights have higher orders

On each level, the node farthest to the right will have the highest order

although there might be other nodes with equal weight

Leaf nodes contain character values, except the Not Yet Transmitted

(NYT) node which is the node whereat all new characters are added

Internal nodes contain weights equal to the sum of their children's

weights

All nodes of the same weight will be in consecutive order.

NYT node is the node with the lowest order in the tree

Tree Manipulation


When a character is read in from a file, the tree is first checked to see if it

already contains that character.

If it doesn't, the NYT node spawns two new nodes. The node to its right is

a new node containing the character and the new left node is the new

NYT node.

If the character is already in the tree, you simply update the weight of that

particular tree node.

In some cases, when the node is not the highest-ordered node in its

weight class, you will need to swap this node so that it fulfills the property

that nodes with higher weight have higher orders. To do this, before you

update the node's weight, search the tree for all nodes of equal weight

and swap the soon-to-be updated value with the highest ordered node of

equal weight. Finally update the weight.


In both cases for inserting values, weights are changed for a leaf and

this change will effect all nodes above it. Therefore, after you insert a

node, you must check the parent above the node following the same

procedure you followed when updating already seen values.

Check to see whether the node in question is the highest order node

in its weight class prior to updating. If not, swap with the node that is

the highest order making sure to reassign only the pointers to the two

nodes being swapped.


NOTE: There are several important checks that need to be in place

prior to any swapping being done:

The root should never be swapped with anything

Remember that you are moving up the tree so things above are

not updated. Therefore, be sure never to swap a node with its

parent.

Although the pointers must be swapped in the tree, be sure to

reset the order to fit the new arrangement. The orders of the two

swapped nodes should not be swapped- or if they are, should be

re-swapped.

Order is not a measure related to the value in a node- it is related

to that node's position in the tree.


In the adaptive Huffman coding procedure, neither transmitter nor receiver

knows anything about the statistics of the source sequence at the start of

transmission. The tree at both the transmitter and the receiver consists of a

single node that corresponds to all symbols not yet transmitted (NYT) and

has a weight of zero. As transmission progresses, nodes corresponding to

symbols transmitted are added to the tree, and the tree is reconfigured using

an update procedure. Before the beginning of transmission, a fixed code for

each symbol is agreed upon between transmitter and receiver.

• Symbol set and their initial codes must be known ahead of time.

• Need NYT (not yet transmitted symbol) to indicate a new leaf is needed in

the tree.

Adaptive Huffman coding


A simple (short) code is as follows:

If the source has an alphabet (a1, a2, . . . , am) of size m, then pick e and r

such that m = 2e+ r and 0 ≤ r < 2e.

The letter ak is encoded as the (e + 1)-bit binary representation of k − 1,

when 1 ≤k ≤2r

else

ak is encoded as the e-bit binary representation of k − r − 1.

For example, suppose m = 26, then e = 4, and r = 10. The symbol a1 is

encoded as 00000, the symbol a2 is encoded as 00001, and the symbol a22

is encoded as 1011.

When a symbol is encountered for the first time, the code for the NYT node is

transmitted, followed by the fixed code for the symbol. A node for the symbol

is then created, and the symbol is taken out of the NYT list.

Adaptive Huffman coding …


Example 1

Assume we are encoding the message [a a r d v a r k], where our

alphabet consists of the 26 lowercase letters of the English alphabet.

We begin with only the NYT node. The total number of nodes in this tree

will be 2 × 26 − 1 = 51, so we start numbering backwards from 51 with the

number of the root node being 51. The first letter to be transmitted is a.

As a does not yet exist in the tree, we send a binary code 00000 for a and

then add a to the tree.

m=24+10

number of bits to encode symbol =4+1=5 bits for symbols <=20

else = 4 bits.


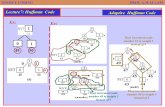
The NYT node gives birth to a new NYT node and a terminal node

corresponding to a. The weight of the terminal node will be higher than the

NYT node, so we assign the number 49 to the NYT node and 50 to the

terminal node corresponding to the letter a.

[a a r d v a r k]

The first letter to be transmitted is a.

As a does not yet exist in the tree, we send

a binary code 00000 for a and then add a to

the tree. (k=1 then a encoded k-1=0)


The second "a" has been read in. "a" is found on the tree and checked to see that

there are no other nodes of equal weight and higher order. There aren't, so "a" is

incremented. The parent of "a" is the root which is never swapped so no more

checking need be done.

"r" is read in. Since "r" is not yet in the tree, the NYT node gives birth to two new

nodes, the left of which becomes the new NYT, and the right the node containing

"r." The old NYT node is checked to see if it is the highest ordered node in its

weight class (parent excluded), and then incremented. Node order 49 is then

checked to see if it is the highest ordered node in it's weight class and is then

incremented when that fact is confirmed. The root is incremented ending the

checking.

[a a r d v a r k]

kr =18, r code = 10001


"d" is read in from the uncompressed file and, as a new node, added to

the tree following the same process as for the insertion of "r." The nodes

along the path from "d" node to the root are checked to make sure they

are the highest ordered nodes in their weight classes and their counts

incremented while moving up the tree.

[a a r d v a r k]


"v" has been read in from the uncompressed file. The file is

completely read. "v" is inserted into the tree in the same manner as

nodes before with the NYT splitting into two leafs- one a new NYT

and the other the leaf with value "v." "v"'s parent is checked and then

incremented.

[a a r d v a r k],


"v"'s parent has been checked and incremented

so we move up to the parent of "v"'s parent,

node of order 47. Before incrementing node 47,

we check and find that node 47 and node 48

both currently have the same weight of 1. But,

because node 47 is about to be incremented, it

should be the highest ordered node in it's

weight class so that when it is incremented it

can move into the next weight class while

preserving the rule that nodes with higher

weights have higher orders. Node 47 and Node

48 are swapped, although the numbering

pattern does not change and they do not swap

orders. All subtrees retain pointers

appropriately. The new Node 48, formerly node

47, is incremented.


Move up the tree to check

node 50. Node 50 is not the

highest node in it's weight

class- node 49 is- so the two

are swapped while keeping

the ordering the same. The

count of the new Node 49,

previously 50, is now

incremented. The parent of

node 49 is the root so there

is no need for any more

checks. The root's count is

incremented.


As we read in the received binary string, we traverse the tree in a

manner identical to that used in the encoding procedure.

Once a leaf is encountered, the symbol corresponding to that leaf is

decoded.

If the leaf is the NYT node, then we check the next e bits to see if the

resulting number is less than r.

If it is less than r , we read in another bit to complete the code for the

symbol.

The index for the symbol is obtained by adding one to the decimal

number corresponding to the e- or e + 1-bit binary string.

Once the symbol has been decoded, the tree is updated and the next

received bit is used to start another traversal down the tree.

Decoding Procedure


The binary string generated by the encoding procedure is

000001010001000001100010110

Decoding Procedure

• Initially, the decoder tree consists only of the NYT node. Therefore, the

first symbol to be decoded must be obtained from the NYT list.

• We read in the first 4 bits, 0000, as the value of e is four. The 4 bits 0000

correspond to the decimal value of 0.

• As this is less than the value of r , which is 10, we read in one more bit

for the entire code of 00000.

• Adding one to the decimal value corresponding to this binary string, we

get the index of the received symbol as 1.

• This is the index for a; therefore, the first letter is decoded as a.

• The tree is now updated.


• The next bit in the string is 1. This traces a path from the root node to

the external node corresponding to a.

• We decode the symbol a and update the tree.

• In this case, the update consists only of incrementing the weight of

the external node corresponding to a.

The next bit is a 0, which traces a path from the root to the NYT node.

The next 4 bits, 1000, correspond to the decimal number 8, which is

less than 10, so we read in one more bit to get the 5-bit word 10001.

The decimal equivalent of this 5-bit word plus one is 18, which is the

index for r . We decode the symbol r and then update the tree.


• The next 2 bits, 00, again trace a path to the NYT node.

• We read the next 4 bits, 0001. Since this corresponds to the decimal

number 1, which is less than 10, we read another bit to get the 5-bit

word 00011.

• To get the index of the received symbol in the NYT list, we add one to

the decimal value of this 5-bit word. The value of the index is 4, which

corresponds to the symbol d.

• Continuing in this fashion, we decode the sequence aardva.


Example 2

Lecture 3 addaptive huffman

Science

Transcript of Lecture 3 addaptive huffman