Solution for Homework 2

ME243A/ECE230A

Fall 2007

Exercise 1

The output of a linear system starting from a non-zero initial state x0 andforced by the input u can be expressed as the sum of two contributions, the freeresponse (x0 6= 0, u = 0) and the forced response (x0 = 0, u 6= 0).

y(t) = yfree(x0, t) + yforced(u, t)

Considering this fact it is seen that only statement (b) is true.

Exercise 2

The ideal low-pass filter is non causal, since g(t) is not zero for t < t0 (Figure1).

Exercise 3

(a)

y[k] = (1)ku[k + 2]

(b)

y[k] = u2[k + 1]

(c)

y[k] = (1)ku2[k 1]

1

2 1.5 1 0.5 0 0.5 1 1.5 2 2.5 34

2

0

2

4

6

8

10

g(t)

t

Figure 1: Impulse response of the ideal low-pass filter ( = 5, t0 = 1).

Exercise 4

(a)

Feeding the input u = u we get the output:

y =

u2(t)u(t 1) u(t 1) 6= 0

0 u(t 1) = 0Since y = y for every u and every real constant , the system is homogeneous.

(b)

Feeding the input u = u1 + u2 we get the output:

y =

(u1(t) + u2(t))2

u1(t 1) + u2(t 1) u1(t 1) + u2(t 1) 6= 00 u1(t 1) + u2(t 1) = 0

Since y 6= y1 + y2 the system is not additive.

(c)

The system is not linear, since linearity requires both homogeneity and additiv-ity.

2

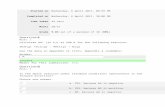
G11

G21

G12

G22

H

u1

u2=y

+y=y

1

+y2=u

Figure 2: Interconnection diagram.

Exercise 5

(a)

The diagram for the interconnection of the two systems is shown in Figure 2.

(b)

Well posedness of the interconnection requires (I G22(s)H(s))1 to exist andbe proper, which means (I G22()H())1 has to exist. Equivalently, (I H(s)G22(s))1 has to exist and be proper.

(c)

W (s) = G11 +G12H(I G22H)1G21Other equivalent solutions are possible (particularly another one that is ob-

tained from this using the matrix identities of Exercise 7).

Exercise 6

(a)

Noting that G22() = D22 and H() = D is it readily seen that the conditionfor well posedness in the state space is that (I D22D)1 has to exist.

3

(b)

Setting = (I D22D)1, and calling x and z the states of systems G and Hrespectively, a state space representation of the interconnected system is givenby the following.[

xz

]=[A1 +B1DC2 B2(I +DD22)C

BC2 A+BD22C

] [xz

]+[B1 +B2DD21

BD21

]u1

y1 =[C1 +D12DC2 D12(I +DD22)C

]+ [D11 +D12DD21]u1

Other equivalent solutions are possible.

Exercise 7

The first identity is proved post-multiplying both sides by (I+MN). The secondidentity is proved post-multiplying both sides by (I+MN) and pre-multiplyingboth sides by post-multiplying both sides by (I +NM).

Using the two identities it is possible to show that:

(I +G2G1)1 = G2(I +G1G2)1G12 (1)

A matrix M(s) of rational functions of s is proper if and only if the quantity

det( limsM(s)) = det(M())

exists and is less than .We can take limit and then determinant of both sides of (1) and use the

following properties:

det(AB) = det(A) det(B)

det(A1) = (detA)1

lims(A(s)B(s)) = A()B().

The third is to be used with care, avoiding indeterminate forms (which will notoccur if A(s) and B(s) are both proper).

We are left with the following:

(I +G2()G1())1 = (I +G1()G2())1

which shows that (I +G2G1)1 is proper if and only if (I +G1G2)1 is proper.

4