Physics 2D : Relativity and Quantum MechanicsSummer Session II, 2013

HOMEWORK #1

SOLUTIONS

All problems can be found in Modern Physics by Randy Harris, Second Edition. Completeall assigned problems; the assignment will be graded based upon completeness and alsothe correctness of one selected problem.

(2.17) Appearing in the time-dilation and length-contraction formulae, γv is a reasonablemeasure of the size of relativistic effects. Roughly speaking, at what speed would obser-vations deviate from classical expectations by 1%?

Solution:

Deviations occur because of a 1% deviation of γ from 1, where γ is the relativistic factorγ =

√1− v2/c2. Then we set

1.01 = 1√1−v

2

c2

⇒ v = 0.14c.

(2.27) Bob and Bob Jr. stand at open doorways at opposite ends of an airplane hangar25 m long. Annie owns a spaceship, 40 m long as it sits on the runway. Annie takes offin her spaceship, then swoops through the hangar at constant velocity. At precisely timezero on both Bob’s clock and Annie’s, Bob sees Annie at the front of her spaceship reachhis doorway. At time zero on his clock, Bob Jr. sees the tail of Annie’s spaceship at hisdoorway. (a) How fast is Annie’s spaceship moving? (b) What will Annie’s clock readwhen she sees the tail of her spaceship at the doorway where Bob Jr. is standing? (c) Howfar will Annie say the front of her spaceship is from Bob at this time?

Solution:

(a) Bob Jr notices the end of Annie’s plane at the coordinates (t = 0, x = -25 m) while Bobmeasures the front of the plane at the same time (in his intertial frame) at (t = 0, x = 0 m).Hence they see Annie’s plane length contracted to the 25 m length of the hangar, and fromthe contraction formula

25m = 40mγ ⇒

2540 =

√1− v2/c2 ⇒ v = 0.781c.

1

(b) What this question really means to ask is what the time reads on the lock at the rearof Annie’s ship as the rear of the ship passes Bob Jr in Annie’s frame. In this case we justhave to apply the Lorentz transformation to Bob Jr’s points at (t=0, x = -25 m). The timeAnnie reads at the back of her ship at this instant is then

t′ = γ(− vc2x+ t) = 1√

1−0.7812

(− 0.781

3×108m/s(−25m) + 0)

= 1.04× 107s = 104ns.

This is a sensible result because it occurs at a time t′= 104 ns, which is after t′=0 s, which iswhen the front of Annie’s ship passes the front of the hangar. In her frame, the rear of herplane should pass by the back of the hangar after the front of her plane passes the front ofthe hangar, since she will not see the two events as simultaneous in her frame.

(c) In Annie’s frame, the hangar is length-contracted to 25 m/γ and passes her at -0.781cto the left. Then when the back of the hangar passes her tail, the front of the hangar is 25m/γ in front of the back of her plane, which is 40 m long in her frame. Then she is 40 m -25 m/γ = 24.375 m in front of Bob at this point (in her frame, of course).

(2.41) A muon has a mean lifetime of 2.2 µs in its rest frame. Suppose muons are travelingat 0.92c relative to Earth. What is the mean distance a muon will travel as measured by anobserver on Earth?

Solution:

In the Earth’s rest frame the muon decay time is dilated from the value in the muon restframe to

∆t = γ∆t0 = 1√1−0.922 (2.2× 10−6s) = 5.61µs.

The distance traveled is then

d = v∆t = (0.92)(3× 108m/s)(5.61× 10−6s) = 1549m.

(2.61) Prove that if v and u′ are less than c, it is impossible for a speed u greater than c toresult from equation (2-19b), the velocity addition formula from special relativity:

u = u′+v

1+u′vc2

.

[Hint: The product (c− u′)(c− v) is positive.]

Solution:

Begin with the hint and massage it into the velocity sum rule:

(c− v)(c− u′) > 0⇒ c2 − (u′ + v)c+ u′v > 0⇒ c2 + u′v > (u′ + v)c⇒ 1 > (u′+v)/c

1+u′vc2

orc > u′+v

1+u′vc2

.

2

In the first step we have expanded the product (c − v)(c − u′) and in the penulatimatestep we have divided both sides by c2(1 + u′v/c2) to get the equation into the form of thevelocity sum rule.

(2.78) Show that the relativistic expression for kinetic energy (γu − 1)mc2 is equivalent tothe classical 1

2mu2 when u� c.

Solution:

Recall the expansion of γ for v � c,

γ = 1√1−v2/c2

≈ 1 +(−1

2

) (−v2

c2

).

Then(γ − 1)mc2 ≈

(1 + 1

2v2

c2− 1)mc2 = 1

2v2

c2mc2 = 1

2mv2.

(2.94) A kaon (denoted K0 is an unstable particle of mass 8.87 × 10−28 kg. One of themeans by which it decays is spontaneous creation of two pions, a π+ and a π−. The decayprocess may be represented as

K0 → π+ + π−

Both the π+ and the π− have mass 2.49× 10−28 kg. Suppose that a kaon moving in the +xdirection decays by this process, with the π+ moving off at speed 0.9c and the π− at 0.8c.(a) What was the speed of the kaon before decay? (b) In what directions do the pions moveafter the decay?

Solution:

(a) Use energy conservation:

γuKmKc2 = γ0.9cmπc

2 + γ0.8cmπc2

1√1−

u2Kc2

= (2.294)(2.49)+(1.67)(2.49)8.87 ⇒ uK = 0.437c

where in the second line we cancelled the common factors of c2 from each energy and thefactor of 10−28 from expressing the mass in kilograms, and γ0.9c = 2.294 and γ0.8c = 1.67.

(b) We use two equation for momentum conservation (canceling all common factors of10−28 from expressing answers in kg):

pi,x = γ0.437c(8.87)(0.437c) = γ0.9c(2.49)(0.9c cos θ1)+γ0.8c(2.39)(0.8c cos θ2)⇒ 3.32 cos θ2 = 4.312−5.141 cos θ1.

and

pi,y = 0 = γ0.9c(2.49)(0.9c sin θ1)− γ0.8c(2.39)(0.8c sin θ2)⇒ 3.32 sin θ2 = 5.141 sin θ1.

3

where the initial momentum in the y-direction is zero and we have written the x- and y-components of the momenta of each pion as the sines and cosines of the angle at whicheach pion shoots out (~v = (v cos θ, v sin θ)). Now we can square both equations and addthem so that we may use the trig identity sin2 x+ cos2 x = 1. Squaring both:

18.591− 44.335 cos θ1 + 26.432 cos2 θ1 = 11.022 cos2 θ2 and 26.432 sin2 θ1 = 11.022 sin2 θ2

and summing (using 11.022(cos2 θ2 + sin2 θ2) = 11.022 and similar for 26.432(sin2 θ1 +cos2 θ1)):

18.591− 44.335 cos θ1 + 26.432 = 11.022⇒ θ1 = 39.9◦.

This angle (small due to the particle moving very fast) is associated to the π+ moving at0.9c. Plugging back in to 5.141 sin θ1 = 3.32 sin θ2, we get θ2 = 83.6◦, associated to the 0.8cπ−.

(2.117) Both clasically and relativistically, the force on an object is what cause a time rateof change of its momentum: F = dp/dt.

(a) Using the relativistically correct expression for momentum, show that

F = γ3umdudt

(b) Under what condition does the classical equation F = ma hold?

(c) Assuming a constant force and that the speed is zero at t = 0, separate t and u, thenintegrate to show that

u = 1√1+(Ft/mc)2

Fm t

[Hint: The following integral may be useful:∫dx

(1−x2)3/2 = x√1−x2 .]

(d) Plot u versus t. What happens to the velocity of an object when a constant force isapplied for an indefinite length of time?

Solution:

(a) We must first use the chain rule to write

ddt = du

dtddu

so that

F = dudt

ddu

(mu√

1−u2/c2

)= du

dt

(m√

1−u2/c2+(−1

2

) (−2 u

c2

)(1− u2/c2)−3/2mu

)= du

dtm

(1−u2/c2)3/2((1− u2/c2) + u2/c2

)= γ3um

dudt .

4

In the first line we used the product rule to differentiate the γ factor separately from the uin the numerator.

(b) In the non-relativistic limit, γ → 1, so γ3 → 1 as well. In this limit, then, F = (1)m · dudt =ma, precisely Newton’s second law.

(c) Multiplying both sides of the full expression from (a) by dt/mwe can arrive an equationto integrate:

Fmdt = du

(1−u2

c2)3/2⇒∫ t

0

Fmdt

′ =

∫ u

0

du′

(1−u′2

c2)3/2

.

The left hand side is simply Ftm , since F/m is constant. The right hand side takes more

work. It calls for a trig substitution. Let u/c = sin θ, so that du = c cos θdθ. Then we canwrite ∫ u

0

du′

(1−u′2

c2)3/2

= c

∫ sin−1(u/c)

0

dθ cos θ(1−sin2 θ)3/2 = c

∫ sin−1(u/c)

0

dθ cos θcos3 θ

= c

∫ sin−1(u/c)

0dθ sec2 θ = c tan θ|sin

−1(u/c)0 = c sin θ√

1−sin2 θ|sin−1(u/c)

0 = u√1−u2/c2

.

In the second line we have used 1 − sin2 θ = cos2 θ. Now we do the algebra to find u as afunction of t:

u√1−u2/c2

= Ftm ⇒ u2 =

(Ftm

)2 (1− u2

c2

)so

u2(

1 +(Ftmc

)2)=(Ftm

)2 ⇒ u = 1√1+(Ft/mc)2

Ftm .

(d) Turn the relation above between u and t into a dimensionless one by dividing by c so

uc = 1√

1+(Ft/mc)2Ftmc = y√

1+y2

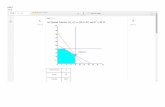
where y is the dimensionless time coordinate y = Ft/mc (we can think of u/c ≡ x as thedimensionless speed coordinate). We can then plot u/c versus y in Figure 1.

(2.118) A rocket maintains a constant thrust F , giving it an acceleration of g (i.e., 9.8 m/s2).(a) If classical physics were valid, how long would it take for the rocket’s speed to reach0.99c? (b) Using the result of Problem 117(c), how long will it really take to reach 0.99c?

Solution:

(a) Classically, we have u = at = gt⇒ t = u/g = 0.99·3×108m/s9.8m/s2

= 3.03× 107s = 0.96 yr.

(b) In the full relativistic result, we must solve the previous equation for t in terms ofu = 0.99c. We put in a = F/m = g and solve

0.99c/c = gt/c√1+(gt/c)2

⇒ (gt/c)2(1− 0.992) = 0.992 ⇒ t = cg

0.99√1−0.992 = 2.15× 108s = 6.8yr.

Relativistic effects require a greater input of energy to approach the speed of light.

5

1 2 3 4y =

Ft

mc

0.2

0.4

0.6

0.8

1.0

u�c

Full relativistic result

Classical result

Figure 1: Plot of u/c versus Ft/mc for constant applied force F in special relavity and inthe classical case.

6