8/14/2019 HW 1 Hand-In Solutions

1/4

SOLUTIONS TO HANDED-IN PROBLEMS OF HOMEWORK 1

(Note: each student solved problem 17.52 online with their individual parameter

values. This solution uses the parameters from the textbook.)

(HW1-A) (0.25 points) Writeup of problem 17.52 from textbook

CALCULATION OF WEIGHT RISE VELOCITY FROM LENGTHS AND ANGULAR

VELOCITIES OF ARM SEGMENTS

Illustrated mechanism represents a persons arm: shoulder is at A, elbow is at B,

hand is at C. The person is pulling a rope which passes over a pulley to lift weight

W.

(1) First we determine the velocity of point B (the elbow). Since AB is a rigid link

rotating around fixed point A with angular velocity AB, VBis given by

VB= (-Yrel)ABi+ (Xrel) ABj

where Xreland Yrelare the x and y coordinates of B with respect to A. In other

words, VB= (-0mm)(1 rad/s)i+ (300mm)(1 rad/s)j

(2) Next we find VCby adding to VBthe velocity of C relative to B, which is a

rotational expression involving BC= 2 rad/s, Xrel= (400mm)cos(60) = 200mm,

and Yrel= (400mm)sin(60) = 346.4mm.

VC= 300 mm/s j + (-346.4mm)(2 rad/s)i+ (200mm)(2 rad/s)j.

= -692.8i+ 700jmm/s

8/14/2019 HW 1 Hand-In Solutions

2/4

(3) We need the unit vector along the rope, which can be derived from the

orientation of the rope (150 degrees from the x axis):

erope= cos(150)i+ sin(150)j= -.8660i+ 0.5j

(4) The dot product VC erope = (-.8660)(-692.8) + (0.5)(700) = 950.0 mm/s

That is the velocity with which C moves away from the pulley. As long as the rope

doesnt stretch, it is also the upwards speed of the weight.

(HW1-B) (0.25 points) Excel calculation of 17.52 result, to give a plot of cable

velocity for 1 second

Here is one way to lay out the calculation. I used about 200 points, and I made the

graph with a smooth curve rather than markers. Speed at 0 is 0.95014, smaller

timesteps should make it even closer to 0.9500 (but such accuracy is rarely

needed).

8/14/2019 HW 1 Hand-In Solutions

3/4

It is interesting to see that the speed rises then falls. What could be happening??

See below.

You were asked to explain why the results lack validity after about 1 second. The

short answer is: because at the given rotation rates of 1 rad/s and 2 rad/s, the

arm segments move to the end of their range of motion!

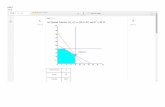
For insight, I plotted the path of the hand (x, y coordinates) at a fairly large time

intervals (note that I stretched the graph to make the axes equal scaleExcel

does not do this automatically). You can see that no person could actually move

their hand that way!

8/14/2019 HW 1 Hand-In Solutions

4/4

From this plot you can see that the path of the hand changes direction, so at

some point it is moving more perpendicular to the cable(thus reducing the

upward velocity of the weight), and later it moves toward the pulley(leading toa negative velocity).