2/15.7293.6

500 cmAFS ===

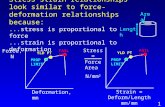
FORCE AND STRESS Pipe routed in straight lines cost the least. Normally, pipe cannot be routed straight because of thermal expansion. Stretching a pipe even a small amount takes a very large force. Preventing pipe from expanding thermally takes an equally large force.

AF

AreaLoadStress ==

Allowable stresses vary with material and temperature, but, are on an order of magnitude of: (a) Pressure = 1,000 to 10,000 psi (6900KPa to 69000KPa_70 2/ cmKg to 700 2/ cmKg ) (b) Deadload = 1,000 to 10,000 psi (6900KPa to 69000KPa 70 2/ cmKg to 700 2/ cmKg ) (c) Thermal = to 20,000 psi (to 138000KPa_ to 1400 2/ cmKg ) The material engineer checks pressure stresses when calculating wall thicknesses. Dead load stresses are controlled by proper use of the pipe span charts and checked by the stress engineer when required. Thermal expansion stresses are roughly determined by piping during the pipe study and finally checked by the stress engineer. Tensile and Compressive Stress

40mm DIA rod 256.12 cmarea =

9000Kg

2/56.71656.12

9000 cmKgAFS ===

500Kg

2 SCH. 40 293.6 cmarea =

Experiments on different materials at different temperatures determine safe stresses. These values are given in the piping code (ASME B31.3_APPENDIX A). Strain (Stretching) is the "unit strain" and is found by dividing the total stretching by the total length being stretched.

001.0

303.0 == (*)

(*) Please, use same units of length for numerator and denominator. Young's Modulus E (Young's Modulus) relates the amount of strain (stretching) to the amount of stress (loading). It is defined as:

SE =

The value of E changes with material and temperature. The stress and strain are measured experimentally. E is calculated and is tabulated in the piping code. E = 30,000,000 psi ( KPax 8102 ; 26 /101.2 cmKgx ) for Cold Steel Normally designed anchors cannot stand large forces because the structure would bend first, and the anchor would not be effective Equipment shells would dimple before they would act as anchors. Expansions are absorbed by bending the piping system rather than compressing it. Thermal Force Between Two Anchors

30m

0.3m stretch

Free Expansion eL= Where is thermal expansion in (mm); e is expansion rate in/100ft (mm/m); L is expansion rate in (mm). The force required to prevent the pipe from expanding is the same as the force required to stretch it an equal amount.

Since AFS = and

SE = and L=

To find F (the force),

Example: For a 6" Sch. 40 Pipe in C.S material at 149C

26 /101.2 cmKgxE = (see B31.3 table C-6) ; mmmmxe /10516.1 3= (see B31.3 table C-1) ; 236cmA = (see characteristic of pipe)

KgxxF 6.1146093610516.1101.2 36 ==

Thermal force on a L-shape pipe fixed at one extremity and guided at other extremity. Example:

EeAAL

eLEAL

EAESAF =====

30m

6m Bending leg

6 SCH 40 C.S. at 260C

To calculate the force against the guide it is possible to use the guided cantilever method:

= 33LEIF

Where

26 /101.2 cmKgxE = (from B31.3 table C-6) ; mm5.903002.3 == (from B31.3 table C-1) ;

41172cmI = (From pipe characteristic table) L=6m

KgF 309= The force against the anchor (indicated by the dotted arrow) is equal to but is pushing in the opposite direction. Thermal force on a Z-shape pipe fixed at both extremities.

Direction Expansion (mm) Leg (m) Force (Kg) A 11x3.83=42.13 7 91 B 7x3.83=26.81 11 15

6m

5m

6 SCH 40 C.S. at 316C

7m

Bending leg for T.F. (Thermal Force) B is the sum of lengths at right angles to the expansion in the direction of B. Thermal force on a pipe connecting vertical vessel to a horizontal vessel.

vB

Radial expansion must be added for vertical vessel. Anchor end of horizontal vessel must be taken into account. If the anchor end and slotted end were reversed, then T.F.A. (thermal force) would be:

Direction Expansion (mm) Leg (m) Force (Kg)

A 9x4.69=42.2 5 642 Reversal of anchor end of horizontal vessel causes an increase in anchor force. Anchor movements are okay to incorporate this way since shell material and temperature are the same as the pipe.

Direction Expansion (mm) Leg (m) Force (Kg) A 5x4.69=23.4 5 356 B 7x4.69=32.8 9 86

4m

5m

5m 2m

Vessels and pipe C.S. material at 371C - pipe 8 sch.40

Thermal force on a Z-shape pipe on piperack S.S. line T =177C 10 sch 20 44736cmI = (see pipe char. Table)

The guide acts as an anchor for forces in "B" direction, but not in "A" direction. Thermal force on pipe connected pump and on piperack

Direction Expansion (mm) Leg (m) Force (Kg) A 23x2.66=61.3 8 357 B 8x2.66=21.3 15 Less than 100

23m 8m 10m

8m

5m

8m

4m 5m

2m 500mm

300mm

300mm

6 sch 40 CS material, T=149C (equipments same material) Force and expansion calculations are the same in plan or elevation. 1. Pump nozzle is not used for flexibility. 2. Pump expansion is included in total expansion. 3. Moving the anchor end is mandatory. 4. Nozzle projections are not used for flexibility here. The stress engineer may include them. The stress and force are checked afterwards, and flexibility is increased only if necessary.

STRESS The formula for calculating stress is (see basic beam formulas):

23

LDES =

Where: S = Stress in PSI ( 2/ cmKg - KPa) E = Modulus of Elasticity = Thermal Growth D = Pipe Diameter L = Length of Bending Leg Guides and anchors have the same effect as in the force calculations. Small diameter piping becomes over stressed before large forces are developed. Large diameter piping creates excessive forces before the piping becomes overstressed.

Direction Expansion (mm) Leg (m) Force (Kg) Horizontal 1.52x9=13.7 6.9 31

Vertical 1.52x7.7=11.7 5 70

Example:

10m 8m

6m

5m

6m

6m

20 C.S. - material T=204C