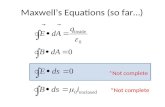__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 1/6

Finite Element Method for Maxwell’s Equations Ferienakademie Sarntal 2007

Course 9: Numerical Simulation: From Models to Software Eugenio Delgado da Carvalheira

1. Maxwell’s Equations

Basically, there is a single set of equations governing all electromagnetic phenomena, Maxwell’s equations. They are comprised of four first-order partial differential equations linking the fundamental electromagnetic quantities, the electric field intensity E (V/m), the magnetic induction B (Vs/m2), the magnetic field intensity H (A/m), the electric flux density D (As/m2), the electric current density J (A/m2), and the space charge density qe (As/m3). The four partial differential equations (PDEs), stated as Maxwell’s equations in differential form are:

.0=⋅∇

=⋅∇∂∂

−=×∇

∂∂

+=×∇

B

qDtBE

tDJH

er

r

rr

rrr

Strictly speaking, these equations are posed over the entire space R3 and they have to be supplemented by the following material laws, where γ denotes the electric conductivity (S/m), Ji an intrinsic current density (A/m2), ε the electric permittivity (As/Vm) and μ the magnetic permeability (Vs/Am):

.

)(

HB

ED

BvEJJ i

r

rr

rrrrr

μ

ε

γ

=

=

×++=

The above combined equations form a set of partial differential equations, linear in space and time, describing the behavior of electromagnetic waves. When electromagnetic fields interact with materials, the equations can assume nonlinear forms. Maxwell’s equations are based on experiments and empirical laws stated by Faraday, Ampère, and Gauss. The great contribution of Maxwell was the unification of the different equations to a set of partial differential equations, and the introduction of the displacement current, which generalizes Ampère’s law.

1.1. Special Cases

In many practical applications one does not have to deal with the full system of Maxwell’s Equations. In special situations assumptions allow substantial simplifications of the model. Most of these assumptions concern the temporal variation of the fields. A special class of time-dependent electromagnetic problems arises, when the displacement currents can be neglected. This is suitable for low-frequency applications, and is called the quasi-static case:

__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 2/6

.

.0

eqDtBE

B

JH

=⋅∇∂∂

−=×∇

=⋅∇

=×∇

r

rr

r

rr

.

)(

ED

BvEJJ

HB

irr

rrrrr

r

ε

γ

μ

=

×++=

=

According to div B = 0, one can show that the magnetic field is solenoidal and therefore can be described by the curl of a vector

.ABrr

×∇= The vector A is called the magnetic vector potential. Substituting into Faraday’s law yields

.0=⎟⎟⎠

⎞⎜⎜⎝

⎛∂∂

+×∇tAEr

r

Thus, we have E = -∂A/∂t and the following curl-curl problem is obtained:

).(1 AvtAJA i

rrr

rr×∇×+

∂∂

−=×∇×∇ γγμ

With more simplifications, namely assuming a static case with no moving bodies (v= 0), and considering a 2D analysis, where Ji is an impressed current in z-direction we obtain the following Poisson problem:

.1. ZZ JA =∇∇−μ

2. Finite Element Method

Numerous different approaches have been used for the numerical treatment of the electromagnetic problem. And several approaches have been explored for the spatial discretization of the field equations. Finite elements provide one of the alternatives for the discretization in space. They rely on approximation spaces for the physical quantities that possess locally supported basis functions. The general approach of the Finite Element Method (FEM) can be resumed as: starting from the partial differential equation (PDE) with given boundary conditions, we multiply it by appropriate test functions and integrate over the whole simulation domain. As a second step, we perform a partial integration and obtain the variational (weak) formulation. At this point, a discretization of the whole domain using finite elements is required. For the discretization triangular as well as quadrilateral finite elements can be used in 2D and tetrahedral as well as hexahedral finite elements in 3D, among others. Applying Galerkin’s approximation method results in the algebraic system of equations. That means, the physical quantity of interest is approximated by functions, called shape functions, and the solution of the algebraic system of equations leads to the physical quantity in the discretization points. For dynamic problems, a time discretization is also required.

__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 3/6

2.1. Weak Formulation

The partial differential equation (PDE) to be solved in its 2D form (derived in the previously section) reads as follows: Given:

.:

: 20

ℜ→Ωℜ→Ω

μA

Find: [ ] 2,0:)( ℜ→×Ω TtA

.1. ZZ JA =∇∇−μ

+ Boundary, interface and initial conditions Now, we convert this formulation into a variational (weak) equation posed over suitable function spaces. We multiply the equation by appropriate test function ψ and apply Green’s first integral theorem, yielding to the following weak formulation: Find 1

0HA∈ , such that

∫∫ ΩΩΩ⋅Ψ=Ω∇Ψ∇ dJdA i)(1)(

μ, .1

0H∈Ψ∀

2.2. Finite Element Discretization

For the discretization of the variational problem, the infinite-dimensional space 10H should be

replaced by a sequence of finite-dimensional spaces. We discretize the domain, using finite elements, and expand the physical quantities in terms of a basis (shape) function. In the Nodal finite element formulation, the quantities are interpolated by the following ansatz, where Nen is the total number of finite element nodes present in the discretization:

ea

ea

h

Nen

eeaa

hx

AxA

ANA

=

⋅= ∑ =

)(1)(

The degrees of freedom are assigned to the node of elements, and the interpolation function (Na), also called shape function, has local support. Local support means that the value of the basis function is weighted in such a way that it is one for the associated node, decay to zero at the neighbor nodes, and has no influence at nodes far away in the grid. Fig.1: 2D mesh Fig.2: 1D basis function

1

__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 4/6

Fig.3: 2D basis function Fig.4: 2D basis function with triangles Nodal elements, as presented above, are constructed to calculate scalar quantities at the nodes of the finite elements.

2.3. Linear System of Equations

Applying the approximation above for both magnetic vector potential (A) and test function (ψ) and substituting in our weak formulation, we obtain a linear system of equations:

fAKrr

=

Where the matrix K, normally called stiffness matrix, has the form:

Ω∇∇= ∫Ω dNNK jT

iij )(1)(μ

Because of the local support characteristic of the basis function, the stiffness matrices obtained are normally sparse. And the right-hand-side, normally called load vector, has the form:

Ω⋅= ∫Ω dJNf iii

For the calculation of the stiffness matrix, integration over the whole domain is necessary. This integral can be approximated by a sum of integrals over each element, what leads to the calculation of “local” stiffness matrix for each element. A numerical integration method should be used to solve this numerically. The same principle is applied for calculation of the load vector. Finally, one can use a solver for the solution of the algebraic system of equations, obtaining the magnetic vector potential at the discretization points.

__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 5/6

3. Discretization with Edge Finite Elements

The use of nodal finite elements for the Poisson problem in the 2D case leads to good results. In 3D calculations, however, where we have the curl-curl problem presented also in section 2.1, the use of nodal finite elements leads to inaccurate results. In this case, one can make use of Edge finite elements. The Edge Elements, also called Nédélec, are defined as vector elements, i.e. the basis functions of these elements represent vector quantities. The degrees of freedom are assigned to the edges of elements, rather than to the nodes. With edge finite elements the magnetic vector potential A is approximated by the following ansatz:

∑=

=≈ne

k

ekk

h AEAA1

where ne defines the number of edges in the finite element mesh, Ek the edge shape function associated with the k-th edge, and e

kA the degree of freedom. The degree of freedom is the line integral of the magnetic vector potential along the k-th edge:

∫ ⋅=k

ek dsAA

r

For tetrahedron elements, one can show that the following interpolation function can be used:

12211 NNNNE ∇−∇= It represents the vector basis function along edge 1 defined by nodes 1 and 2, and N1 and N2 the nodal basis function in node 1 and 2, respectively. To obtain for the tangential component of Ek the value 1, we have to scale the vector function with the length of the corresponding edge, resulting in the following set of edge finite elements for the tetrahedron:

Fig.5: Tetrahedral edge element

.)()()()()()(

634436

542245

423324

314413

213312

112211

lNNNNElNNNNElNNNNElNNNNElNNNNElNNNNE

∇−∇=∇−∇=∇−∇=∇−∇=∇−∇=∇−∇=

__________________________________________________________________________________________

Finite Element Method for Maxwell’s Equation 6/6

4. Simulation Example

In the following example, we performed a simulation using the finite element method with both nodal finite elements and edge finite elements. At this example we considered the calculation of the magnetic induction within a ferromagnetic cube surrounded with air. A parameter jump in the magnetic permeability across the cube/air interface by a factor of 1000 is assumed. The boundary conditions for the magnetic vector potential are applied in such a way that we would expect a uniform magnetic induction within the ferromagnetic cube. Both discretization methods (nodal and edge finite elements) were used and the results presented below. We can observe that the calculation with nodal elements results in a non-uniform field.

Fig.6: Nodal elements Fig.7: Edge elements

References

1. M. Kaltenbacher, Numerical Simulation of Mechatronic Sensor and Actuators,

Springer-Verlag Berlin Heidelberg, 2004.

2. S. Zaglmayr, High Order Finite Element Methods for Electromagnetic Field Computation, Dissertation, Universität Linz, 2006.

3. R. Beck, P. Deuflhard, R. Hiptmair, R. H. W. Hoppe, B. Wohlmuth, Adaptive multilevel

methods for edge element discretizations of Maxwell’s equations, Springer-Verlag, Surveys on Mathematics for Industry (1999) 8: 271-312.