Example 1 Estimate by the six Rectangle Rules using the regular
3
1 Example 1 Estimate by the six Rectangle Rules using the regular partition P of the interval [0,1] into 4 subintervals. Solution This definite integral gives the area of a quarter circle of radius 1 and therefore has value /4. Hence estimating this integral means estimating the value of /4. Note that P = {0, ¼, ½, ¾, 1} with each subinterval of width ¼. The four subintervals are: [0, ¼ ], [¼, ½], [½,¾] and [¾, 1] while the function is Then The L k are the heights of the 4 rectangles used to approximate this definite integral. dx x 1 1 0 2 . ) ( 2 x 1 x f . 4 3 2 1 1 0 2 L L L L 4 1 dx x 1 In the Left Endpoint Rule the L k are the values of f on the left endpoints of the four subintervals: f(0), f(¼), f(½), f(¾). In the Right Endpoint Rule the L k are the values of f on the right endpoints of the four subintervals: f(¼), f(½), f(¾), f(1). y x 1 0 2 x 1 y
description
Example 1 Estimate by the six Rectangle Rules using the regular partition P of the interval [ 0,1 ] into 4 subintervals. - PowerPoint PPT Presentation
Transcript of Example 1 Estimate by the six Rectangle Rules using the regular
1
Example 1 Estimate by the six Rectangle Rules using the regular
partition P of the interval [0,1] into 4 subintervals.
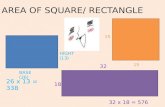
Solution This definite integral gives the area of a quarter circle of radius 1 and therefore has value /4. Hence estimating this integral means estimating the value of /4. Note that P = {0, ¼, ½, ¾, 1} with each subinterval of width ¼. The four subintervals are:
[0, ¼ ], [¼, ½], [½,¾] and [¾, 1]
while the function is Then
The Lk are the heights of the 4 rectangles used to approximate this definite integral.
dxx11
0
2
.)( 2x1xf
. 4321
1
0
2 LLLL41
dxx1
In the Left Endpoint Rule the Lk are the values of f on the left endpoints of the four subintervals: f(0), f(¼), f(½), f(¾). In the Right Endpoint Rule the Lk are the values of f on the right endpoints of the four subintervals: f(¼), f(½), f(¾), f(1).
y
x10
2x1y
2
In the Midpoint Rule the Lk are the values of f on the midpoints of the four subintervals: f(1/8), f(3/8), f(5/8), f(7/8).
In the Trapezoid Rule the Lk are the averages of the values of f on the endpoints of each of the four subintervals:
½[f(0)+f(¼)], ½[f(¼)+f(½)], ½[f(½)+f(¾)], ½[f(¾)+f(1)].
Therefore, the Lower Riemann sum coincides with the estimate of the Right Endpoint Rule and the Upper Riemann sum coincides with estimate of the Left Endpoint Rule.
Since the function f is decreasing on [0,1], it has its maximum value at the left endpoint of each subinterval and its minimum value at the right endpoint of each subinterval.
The values of the Lk are summarized in the table on the next slide
The 4 subintervals are: [0, ¼ ], [¼, ½], [½,¾], [¾, 1].
y
x10
2x1y
3
The Left Endpoint Rule and Upper Riemann Sum give the same estimate:
The Right Endpoint Rule and Lower Riemann Sum give the same estimate:
The Midpoint Rule gives the estimate:
The Trapezoid Rule gives the estimate:
874.0661.866.968.14
1
4
1 1
4 4321
1
0
2 LLLLdxx
624.00661.866.968.4
1
4
1 1
4 4321
1
0
2 LLLLdxx
796048478192799241
LLLL41
dxx14 4321
1
0
2 .....
749.0331.764.917.984.4
1
4
1 1
4 4321
1
0
2 LLLLdxx
Left
Endpoint Rule
Right
Endpoint
Rule
Midpoint Rule
Trapezoid Rule
Lower
Riemann
Sum
Upper
Riemann
Sum
L1
L2
L3
L4
f(0)=1
f(¼).968
f(½) .866
f(¾) .661
f(¼).968
f(½) .866
f(¾) .661
f(1)=0
f(1/8) .992
f(3/8) .927
f(5/8) .781
f(7/8) .484
½(1+.968)
½(.968+.866)
½(.866+.661)
½(.661+0)
f(¼).968
f(½) .866
f(¾) .661
f(1)=0
f(0)=1
f(¼).968
f(½) .866
f(¾) .661
