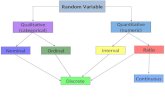
Random variables can be classified as either discrete or continuous.

Example: Discrete: mostly counts Continuous: time, distance, etc.

1. They are used to describe different types of quantities.

2. We use distinct values for discrete random variables but continuous real numbers for continuous random variables.

3. Numbers between the values of discrete random variable makes no sense, for example, P(0)=0.5, P(1)=0.5, then P(1.5) has no meaning at all. But that is not true for continuous random variables.

Both discrete and continuous random variables have sample space.

For discrete r.v., there may be finite or infinite number of sample points in the sample space.

For continuous r.v., there are always infinitely many sample points in the sample space.

*** For discrete r.v., given the pmf, we can find the probability of each sample point in the sample space.

*** But for continuous r.v., we DO NOT consider the probability of each sample point in the sample space because it is defined to be ZERO!

In another word, For discrete random variables, only the

value listed in the PMF have positive probabilities, all other values have probability zero. We can find probability for some specific value or an interval of values.

For continuous random variables, the probability of every specific value is zero. Probability only exists for an interval of values for continuous r.v..

Let X be the number of stops for a citybus going from downtown Lafayette to Purdue campus. X is a discrete/continuous?

Let Y be the distance from the train station and where a citybus can stop at when it comes from downtown Lafayette to Purdue campus. Y is a discrete/continuous?

P(X=3 stops)=? P(Y=150 yards)=?

PDF and CDF. PDF is Probability Density Function, it is

similar to the PMF for discrete random variables, but unlike PMF, it does not tell us about the probability.

CDF is Cumulative Distribution Function, it has a counterpart for discrete random variables, but for continuous random variables, it is the only way we can find a probability.

For discrete random variables: PMF: P(X=K) CDF: P(a < X < b) = ∑KP(X=K)

For continuous random variables: PDF: f(x) CDF: F(x)=P(a < X < b) = ∫a

b f(x)dx

For discrete random variables, both PMF and CDF can tell us probabilities.

For continuous random variables, ONLY CDF can tell us probabilities.

Given X is a continuous random variable with sample space Ω and its PDF is f(x), f(x) must satisfy the following conditions: 1. 0≤ f(x) 2. ∫Ωf(x) dx= 1 The same as the conditions for discrete random

variables.

A continuous random variable X has the pdf f(x)=c(x-1)(2-x) over the interval [1, 2] and 0 elsewhere. What value of c makes f(x) a valid pdf for X?

What is P(x>1.5)?

Think about the citybus example and simplify it. Suppose the citybus starts at point A and goes toward point B, if this bus can stop at will, or stop at each point between A and B with equal probability, we let X be the distance between where the bus stops and point A.

Then X is a random variable and it is said to follow a Uniform distribution.

We will talk about several continuous distributions, we need to know: Their PDF How to calculate probability under those

distributions. How to find mean and variance for those random

variables

For Uniform: PDF:

In order to calculate the probability, we need to know the distance between A and B.

In another word, the parameters for a uniform distribution are A and B in this case, where A and B are defined as the distance mark for the two points.

1 ,( )

0,

A X Bf x B A

elsewhere

For example, if B is 2000 yards away from A, then B-A=2000.

And the probability that the bus stops within 200 yards from A would be

200 200

0 0

1 200( ) 0.12000 2000

f x dx dx

Then what is the probability that the bus stops somewhere between 400 yards away from A and 600 yards away from A?

600 600

400 400

1 200( ) 0.12000 2000

f x dx dx

What is the probability that the bus stops within 200 yards away from point B?

2000 2000

1800 1800

1 200( ) 0.12000 2000

f x dx dx

What is the probability that the bus stops half way between A and B.

1000 1000

0 0

1 1000( ) 0.52000 2000

f x dx dx

Given that a continuous r.v. follows a uniform distribution with pdf:

1 ,( )

0,

a X bf x b a

elsewhere

( )2a bE X

2( )( )12b aVar X

Let T be the time when a STAT225 student turned in his/her exam 1 hour after the exam started. Suppose this time is uniformly/evenly distributed between 9pm and 9:30pm.

What is the pdf of T?

What is the probability that a student turned in the exam between 9:10pm and 9:25pm?

What is the mean and standard deviation of T?

What is the probability that a student turned in the exam at 9:30pm?

What is the probability that a student turned in the exam by 9:30pm?