1 I. SUPPLEMENTARY MATERIAL 1: entations. This …10.1038...1 I. SUPPLEMENTARY MATERIAL 1:...
Transcript of 1 I. SUPPLEMENTARY MATERIAL 1: entations. This …10.1038...1 I. SUPPLEMENTARY MATERIAL 1:...
![Page 1: 1 I. SUPPLEMENTARY MATERIAL 1: entations. This …10.1038...1 I. SUPPLEMENTARY MATERIAL 1: COMPARISON OF SIMULATIONS WITH REAL SNOWFLAKES (a) Simple star from [1] (b) Simple star (c)](https://reader031.fdocuments.in/reader031/viewer/2022022007/5ad23b847f8b9a72118ce27d/html5/thumbnails/1.jpg)
1
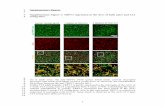
I. SUPPLEMENTARY MATERIAL 1:COMPARISON OF SIMULATIONS WITH REAL
SNOWFLAKES
(a) Simple star from [1] (b) Simple star
(c) Stellar dendrite from [1] (d) Stellar dendrite
(e) Sectored plate from [1] (f) Sectored plate
FIG. 1. Comparison between real snowflakes photographs(left) taken from [1], and our phase field simulations (right).Visual rendering for our simulations uses the softwareBlender.
SUPPLEMENTARY MATERIAL 2: 3DFACETING ALGORITHM
Faceting requires the anisotropy constants εxy and εzvalues in A(n), to exceed 1/35 for 6-fold horizontal sym-metry, and 1/3 for 2-fold vertical symmetry [2]. Abovesuch values, metastable and unstable crystal orientationsn where the stiffness becomes negative, emerge. A(n)must hence be modified, so that the stiffness remainspositive. A preliminary step is to determine missing ori-
entations. This can be done by detecting sign change inthe stiffness. This causes a local convexity inversion inthe 2D polar plot of 1/A(θ, φ0), for any fixed azimuthalangle φ0, or in the polar plot of 1/A(θ0, φ) for any fixedpolar angle θ0. This reads A+∂2θθA = 0 and A+∂2φφA = 0respectively, providing us with the maximum anisotropyconstants εmxy and εmz before missing orientation:
εmxy =
1 + εz cos(2φ)
35
εmz =1 + εxy cos(6θ)
3.
(1)
Restricting the study to θ ∈ [−π/6, π/6] and φ ∈ [0, π]due to rotation periodicity of A(θ, φ), missing θ orienta-tions lie within a φ-dependant angular sector [−θm(φ) +kπ/3, θm(φ) + kπ/3] (k ∈ Z) for εxy > εmxy. Same goesfor φ orientations lying within [−φm(θ) + kπ, φm(θ) +kπ] for εz > εmz . Following the procedure developedby Eggleston in [3], θm and φm respectively satisfy∂θ[cos(θ)/A(θ, φ)] = 0 and ∂φ[cos(φ)/A(θ, φ)] = 0, lead-ing to:
6εxy sin(6θm) cos(θm)
sin(θm)= (1 + εxy cos(6θm) + εzcos(2φ))
2εz sin(2φm) cos(φm)
sin(φm)= (1 + εxy cos(6θ) + εzcos(2φ
m)) .
(2)The regularization step finally consists in replacingA(θ, φ) by a simple trigonometric function for missingorientation, as suggested by Debierre et al. [4]:
A(n) =
Aθ(θ, φ) = A1(φ) +B1 cos(θ), |θ| < θm, |φ| ≥ φm
Aφ(θ, φ) = A2(θ) +B2 cos(φ), |θ| ≥ θm, |φ| < φm
α(θ, φ)Aθ + (1− α(θ, φ))Aφ, |θ| < θm, |φ| < φm
1 + εxy cos(6θ) + εz cos(2ψ) otherwise.(3)
Coefficients A1(φ), B1, A2(θ), B2 and α(θ, φ) are set toensure continuity of A(n) and its derivatives:
A1(φ) = 1 + εxy cos(6θm) + εz cos(2φ)− 6εxy sin(6θm)
sin(θm)cos(θm)
B1 =6εxy sin(6θm)
sin(θm)
A2(θ) = 1 + εxy cos(6θ) + εz cos(2φm)− 2εz sin(2φm)
sin(φm)cos(φm)
B2 =2εz sin(2φm)
sin(φm)
α(θ, φ) =|θ − θm|√
(θ − θm)2 + (φ− φm)2.
(4)
![Page 2: 1 I. SUPPLEMENTARY MATERIAL 1: entations. This …10.1038...1 I. SUPPLEMENTARY MATERIAL 1: COMPARISON OF SIMULATIONS WITH REAL SNOWFLAKES (a) Simple star from [1] (b) Simple star (c)](https://reader031.fdocuments.in/reader031/viewer/2022022007/5ad23b847f8b9a72118ce27d/html5/thumbnails/2.jpg)
2
[1] K. G. Libbrecht, “Snowcrystals.com,” http://www.
snowcrystals.com.[2] I. Singer-Loginova and H. Singer, Reports on progress in
physics 71, 106501 (2008).
[3] J. J. Eggleston, G. B. McFadden, and P. W. Voorhees,Physica D: Nonlinear Phenomena 150, 91 (2001).
[4] J.-M. Debierre, A. Karma, F. Celestini, and R. Guerin,Physical Review E 68, 041604 (2003).