1 © 2010 Pearson Education, Inc. All rights reserved 10.1 DEFINITION OF A SEQUENCE An infinite...

1© 2010 Pearson Education, Inc. All rights reserved

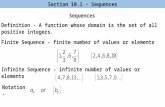
10.1 DEFINITION OF A SEQUENCEAn infinite sequence is a function whose domain is the set of positive integers. The function values are called the terms of the sequence. The nth term, an, is called the general term of the sequence.

a1, a2, a3, a4, … , an, …,

1 11

n

nbn

1 1 2

1

11 1 1 1

1b

2 1 3

2

1 1 11 1

2 2 2b

3 1 4

3

1 1 11 1

3 3 3b

4 1 5

4

1 1 11 1

4 4 4b

6 1 7

6

1 1 11 1

6 6 6b

5 1 6

5

1 1 11 1

5 5 5b


Finding a General Term of a Sequence from a Pattern

Write the general term an for a sequence whose first five terms are given.

To do this, write the position number of the term above each term of the sequence and look for a pattern that connects the term to the position number of the term.

Apparent pattern: Here 1 = 12, 4 = 22, 9 = 32, 16 = 42, and 25 =52. Each term is the square of the position number of that term. This suggests an = n2.

Apparent pattern: When the terms alternate in sign and n = 1, use factors such as (−1)n if we want to begin with the factor −1 or we use factors such as (−1)n+1 to begin with the factor 1.


RECURSIVE FORMULASA recursive formula requires that one or more of the first few terms of the sequence be specified and all other terms be defined in relation to previously defined terms.

The Fibonacci sequence is a famous sequence that is defined recursively and shows up often in nature. In this sequence, we specify the first two terms as a0 = 1 and a1 = 1; each subsequent term is the sum of the two terms immediately preceding it.

1 1 2 3 5 8…ak , where ak-2 + ak-1

Write the first five terms of the recursively defined sequence a1 = 4, an+1 = 2an – 9

We are given the first term of the sequence: a1 = 4.a2 = 2a1 – 9 = 2(4) – 9 = –1a3 = 2a2 – 9 = 2(–1) – 9 = –11a4 = 2a3 – 9 = 2(–11) – 9 = –31a5 = 2a4 – 9 = 2(–31) – 9 = –71

So the first five terms of the sequence are:4, –1, −11, −31, −71


DEFINITION OF FACTORIALFor any positive integer n, n factorial (written n!) is defined as

! 1 4 3 2 1.n n n 0! 1.and

= 16 · 15 = 240

= (n + 1) n


SUMMATION NOTATIONThe sum of the first n terms of a sequence a1, a2, a3, …, an, … is

The letter i in the summation notation is called the index of summation, n is called the upper limit, and 1 is called the lower limit, of the summation.

1 2 31

.n

i ni

a a a a a

9

1

2 3 4 41 95 6 7 8 5i

i

2 22

2

4

2

7

2 1 2 1 2 1

2 1 2 1

31 49 71 97

4

7

5

6

248

j

j

0 41 2 34

0 0 4

2 2 2 2 2 2

! ! ! ! ! !

1 2 4 8 16

1 1 2 6 244 2

1

3

23

1

2 73

2

k

k k

6

SUMMATION PROPERTIES

© 2010 Pearson Education, Inc. All rights reserved


DEFINITION OF A SERIESLet a1, a2, a3, … , ak, … be an infinite sequence. Then

1. The sum of the first n terms of the sequence is called the nth partial sum of the sequence and is denoted by

1 2 31

.n

n ii

a a a a a

(This sum is a finite series.)

2. The sum of all terms of the infinite sequence is called an infinite series and is denoted by

1 2 31

.n ii

a a a a a


Writing a Partial Sum in Summation Notation

Write each sum in summation notation.

3 5 7 21 a.

10

1

3 5 7 21 2 1k

k

a. This is the sum of consecutive odd integers from 3 to 21. Each can be expressed as 2k + 1, starting with k = 1 and ending with k = 10.

1 1 1

4 9 49 b.

b. This finite series is the sum of fractions, each of which has numerator 1 and denominator k2, starting with k = 2 and ending with k = 7.

7

22

1 1 1 1

4 9 49 k k


10.2 DEFINITION OF AN ARITHMETIC SEQUENCE

The sequence a1, a2, a3, a4, … , an, …is an arithmetic sequence, or an arithmetic progression if there is a number d such that each term in the sequence except the first is obtained from the preceding term by adding d to it. The number d is called the common difference of the arithmetic sequence. We have

d = an + 1 – an, n ≥ 1.

An arithmetic sequence a1, a2, a3, a4, … , an, … can be defined recursively. The recursive formula

an + 1 = an + d for n ≥ 1defines an arithmetic sequence with first term a1 and common difference d.

If a sequence a1, a2, a3, … is an arithmetic sequence, then its nth term, an, is given by an = a1 + (n – 1)d where a1 is the first term and d is the common difference.


Common Difference of an Arithmetic Sequence

Example: Find the common difference d and the nth term an of an arithmetic sequence whose 5th term is 15 and whose 20th term is 45.

1

1

1

1

4 20

45 19

5 1

n a d

a

a d

n

d

a

1

1

1

1

5 1

15 4

15

n a d

a d

a

a d

n

1

7

1

1

7 2 2

2

2 5

n

n

n

a n

a n

a n n

da

The nth term is given by an = 2n + 5, n ≥ 1.

Solving the system of equations gives a1 = 7 and d = 2.


SUM OF n TERMS OF AN ARITHMETIC SEQUENCE

Let a1, a2, a3, … an be the first n terms of an arithmetic sequence with common difference d. The sum Sn of these n terms is given by

where an = a1 + (n – 1)d.1 ,2

nn

a aS n

Example: Find the sum of the arithmetic sequence of numbers:1 + 4 + 7 + … + 25

Arithmetic sequence with a1 = 1 and d = 3. First find the number of terms.

1 1

1 1

24 3

35

1

2

n a n

n

n

a d

1

9 9

2

2

25

9 13 117

1

nnS

S

aan

Thus 1 + 4 + 7 + … + 25 = 117.


10.3 DEFINITION OF A GEOMETRIC SEQUENCE

The sequence a1, a2, a3, a4, … , an, …is a geometric sequence, or a geometric progression, if there is a number r such that each term except the first in the sequence is obtained by multiplying the previous term by r. The number r is called the common ratio of the geometric sequence.

1 , 1n

n

ar n

a Thus, an + 1 = ran, n ≥ 1

Every geometric sequence can be written in the forma1, a1r, a1r2, a1r3, … , a1rn−1, …

Since a1 = a1(1) = a1r0, the nth term of the geometric sequence isan = a1rn–1, for n ≥ 1.

Example1: Geometric sequence 1, 3, 9, 27, … Find a1, r, and an

a1 = 1 (1st term)r = 9/3 (ratio of consecutive terms) = 3An = a1rn-1 = (1)(3n-1)=3n-1

Example2: Find the 23rd termof a geometric sequence with first term 10 & common ratio 1.2 An = a1rn-1 = (10)(1.2)23-1 = 552.06


SUM OF THE TERMS OF A FINITE GEOMETRIC SEQUENCE

Let a1, a2, a3, … an be the first n terms of a geometric sequence with first term a1 and common ration r. The sum Sn of these terms is

111

1

1, 1.

1

nni

ni

a rS a r r

r

Examples: Find the sum of

a. A1 = 5, r = .7, n = 15

15 15

1

1 1

5 0.7 5 0.7i i

i i

a. b.

1515

115 1

1

1 0.75 16.588

1 0.7i

i

S a r

15 15

1

1 1

5 0.7 0.7 5 0.7i i

i i

b.

0.7 16.588

11.6116


SUM OF THE TERMS OF AN INFINITE GEOMETRIC SEQUENCE

If |r| < 1, the infinite sum a1 + a1r + a1r2 + a1r3 + … + a1rn–1 + … is

Example: Find the sum 3 9 27

2 .2 8 32

1 82

41 3

1rS

a


10.5 Binomial Theorem & PASCAL’S TRIANGLE


BINOMIAL EXPANSIONSThe patterns for expansions of (x+ y)n (with n = 1, 2, 3, 4, 5) suggest:

1. The expansion of (x+ y)n has n + 1 terms.

2. The sum of the exponents on x and y in each term equals n.

3. The exponent on x starts at n (xn = xn · y0) in the first term and decreases by 1 for each term until it is 0 in the last term (x0 · yn = yn).

4. The exponent on y starts at 0 in the first term (xn = xn · y0) and increases by 1 for each term until it is n in the last term (x0 · yn = yn).

5. The variables x and y have symmetrical roles. That is, replacing x with y and y with x in the expansion of (x+ y)n yields the same terms, just in a different order.

• Coefficients of 1st & last terms are both 1• Coefficients of the second and the next-to-last terms are equal. • In general the coefficients of xn−jyj and xjyn−j are equal for j = 0, 1, 2, …, n. • Coefficients in binomial expansion of (x + y)n are the binomial coefficients.• Coefficients of each term of (x + y)n can be determined using Pascal’s Triangle. • Top row represents coefficients of (x + y)0, Next row (x + y)1, etc.


Example: Expand (4y – 2x)5.

The fifth row of Pascal’s Triangle yields coefficients 1, 5, 10, 10, 5, 1.

Replace x with 4y and y with –2x.

Using Pascal’s Triangle to Expand a Binomial Power

554 2x y y x

5 4 3 2

2 3 4 5

1024 2560 2560

1280 320 32

y y x y x

y x yx x

5 4 3 2

2 3 4 5

4 5 4 2 10 4 2

10 4 2 5 4 2 2

y y x y x

y x y x x

18

Ti 83/84

5 C

3 = 5 [Math][PRB][nCr][Enter] 3

!

( )! !n r

nC

n r r

n

r

=

Evaluating Binomial Coefficients/Combinations


THE BINOMIAL THEOREMIf n is a natural number, then the binomial expansion of (x + y)n is given by

1 2 2

0 1 2n n n n

n r r n

n n nx y x x y x y

n nx y y

r n

0

.n

n r r

i

nx y

r

Example: Find the binomial expansion of (x – 3y)4.(x – 3y)4 = [x + (–3y)]4

4


PARTICULAR TERM IN A BINOMIAL EXPRESSION

The term containing the factor xr in the expansion of (x + y)n is

Example: Find the term containing x10 in the expansion of (x + 2a)15 .

15 1010152

15 10r n rn

x y x an r

510152

5x a

10 5 515!

25! 15 5 !

x a

10 5

10 5

10 5

15!32

5! 10 !

15 14 13 12 11 10!32

5! 10!

96,096

x a

x a

x a


10.4 Using Mathematical Induction

Use mathematical induction to prove that, for all natural numbers n,

2 4 6 2 1 .n n n

First: Verify that the statement is true for n = 1.

Second: Assume the formula is true for k2 + 4 + 6 + … + 2k

= k(k + 1)

2

1

2

1 12 1

Third: On the basis the formula is true for k, show it is true for k+1, which means start from the second step above and show the following statement is true.

2 + 4 + 6 + … + 2(k+1) = (k + 1)(k + 1 + 1)

2 + 4 + 6 + … + 2k + 2(k+1) = k(k+1) + 2(k+1)2 + 4 + 6 + … + 2k + 2(k+1) = (k + 1)(k + 2)2 + 4 + 6 + … + 2k + 2(k+1) = (k + 1)(k + 1 + 1)

Thus, by induction, the formula is true for for all natural numbers, n.


Mathematical Induction Continued…

Thus, by induction, 2k+1 > k + 1 is true so 2n+1 > n for all natural numbers, n.

Use mathematical induction to prove for all natural numbers that 2n n

21 1First: Verify that the statement is true for n = 1.

Second: Assume the formula is true for k 2k > k

Third: On the basis the formula is true for k, show it is true for k+1, which means start from the second step above and show the following statement is true.

2k+1 > k+1 [Note: 2k+1 > (2k)(21) ]

2k ∙ 21 > k ∙ 21 2k ∙ 2 > 2k 2k = k + k ≥ k + 1

1 © 2010 Pearson Education, Inc. All rights reserved 10.1 DEFINITION OF A SEQUENCE An infinite...

Documents

Transcript of 1 © 2010 Pearson Education, Inc. All rights reserved 10.1 DEFINITION OF A SEQUENCE An infinite...